Mahan excitons in room-temperature methylammonium lead bromide perovskites

Abstract

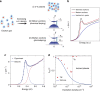
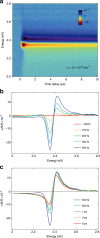
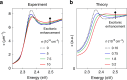
In a seminal paper, Mahan predicted that excitonic bound states can still exist in a semiconductor at electron-hole densities above the insulator-to-metal Mott transition. However, no clear evidence for this exotic quasiparticle, dubbed Mahan exciton, exists to date at room temperature. In this work, we combine ultrafast broadband optical spectroscopy and advanced many-body calculations to reveal that organic-inorganic lead-bromide perovskites host Mahan excitons at room temperature. Persistence of the Wannier exciton peak and the enhancement of the above-bandgap absorption are observed at all achievable photoexcitation densities, well above the Mott density. This is supported by the solution of the semiconductor Bloch equations, which confirms that no sharp transition between the insulating and conductive phase occurs. Our results demonstrate the robustness of the bound states in a regime where exciton dissociation is otherwise expected, and offer promising perspectives in fundamental physics and in room-temperature applications involving high densities of charge carriers.

Fig. 1. Absorption spectra and exciton ionization ratio.

a Evolution of the bound exciton gas in a bulk semiconductor with increasing carrier density. Two scenarios are possible: (i) bound excitons are ionized into an e–h plasma and the Mott transition to a metallic state takes place; (ii), (iii) e–h correlations still persist in the form of Mahan excitons, i.e. bound states in the Fermi sea in a (ii) chemically-doped and (iii) photodoped semiconductor. E_F indicates the Fermi energy; E_F,c and E_F,v represent the quasi-Fermi energies of the conduction band and valence band, respectively. b Schematic representation of the optical absorption spectrum of a bulk semiconductor in the presence of Wannier excitons (black curve), and its modification at high carrier densities. The Mott transition manifests itself with the ionization of the Wannier exciton (blue curve), whereas the Mahan exciton scenario features the persistence of the Wannier peak and the enhancement of the absorption continuum (red curve). c Absorption spectrum of CH₃NH₃PbBr₃ single crystals as obtained from the ellipsometry data (dots), fitted with Elliott theory (solid line) and resulting in a binding energy E_b = 71 meV, linewidth Γ = 34 meV, and single-particle gap energy E_g = 2.42 eV. The blue and red dotted lines represent the distinct contributions of the Wannier exciton and the continuum, respectively. d Exciton ionization ratio as a function of the excitation density, where n_free∕n = 0 corresponds to an exciton gas and n_free∕n = 1 to a fully ionized plasma, as calculated from the theory of ionization equilibrium (TIE, red dots). The vertical line indicates the Mott critical density, found at n_M ~ 8 × 10¹⁷ cm⁻³. The solid line represents the ionization ratio calculated with the Saha equation, and it is added for comparison.

Fig. 2. Ultrafast transient reflectivity measurements.

a Color-coded map of ΔR∕R as a function of probe photon energy and time delay between pump and probe. The pump photon energy is 3.10 eV and the estimated carrier density is n = 5 × 10¹⁸ cm⁻³. The time resolution is 50 fs. b, c ΔR∕R transient spectra in the temporal windows b from −100 fs to 500 fs and c from 500 fs to 8 ps.

Fig. 3. Reflectivity lineshape analysis.

a–c Temporal evolution of the oscillator strength (ΔOS, a), peak position (ΔE_x, b) and linewidth (ΔΓ, c), obtained through the fit of ΔR∕R(ω, t) at the excitation density of n = 5 × 10¹⁸ cm⁻³. d, e Evolution of the absorption spectra α(ω, t) of CH₃NH₃PbBr₃ single crystals in the vicinity of the excitonic resonance as calculated with the Tauc-Lorentz fit of ΔR∕R(ω, t) in the temporal windows (d) from 0 fs to 500 fs and (e) from 500 fs to 8 ps.

Fig. 4. Comparison between experimental and theoretical absorption spectra.

a Experimental absorption spectrum of CH₃NH₃PbBr₃ single crystals for the excitation densities of 5, 7.5 and 10 × 10¹⁸ cm⁻³ at 1 ps. Similar trends can be observed at any time delay between 500 fs and several ps. b Theoretical absorption spectra of CH₃NH₃PbBr₃ in the presence of increasing carrier densities, as calculated with the SBE. The black arrow indicates the excitonic enhancement of the above-gap absorption associated with the presence of e–h correlations in the highly photoexcited material. In both cases, the Wannier bound exciton peak persists above n_M.