Sparse identification of contrast gain control in the fruit fly photoreceptor and amacrine cell layer

Abstract

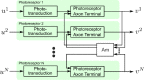
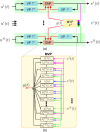
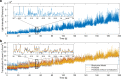
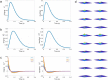
The fruit fly's natural visual environment is often characterized by light intensities ranging across several orders of magnitude and by rapidly varying contrast across space and time. Fruit fly photoreceptors robustly transduce and, in conjunction with amacrine cells, process visual scenes and provide the resulting signal to downstream targets. Here, we model the first step of visual processing in the photoreceptor-amacrine cell layer. We propose a novel divisive normalization processor (DNP) for modeling the computation taking place in the photoreceptor-amacrine cell layer. The DNP explicitly models the photoreceptor feedforward and temporal feedback processing paths and the spatio-temporal feedback path of the amacrine cells. We then formally characterize the contrast gain control of the DNP and provide sparse identification algorithms that can efficiently identify each the feedforward and feedback DNP components. The algorithms presented here are the first demonstration of tractable and robust identification of the components of a divisive normalization processor. The sparse identification algorithms can be readily employed in experimental settings, and their effectiveness is demonstrated with several examples.

Keywords: Contrast gain control; Divisive normalization; Fruit fly; Photoreceptor; Sparse functional identification.

Figure 1

A schematic diagram of interaction between Amacrine cells and photoreceptors in multiple cartridges

Figure 2

Schematic diagram of a temporal divisive normalization processor

Figure 3

Schematic block diagram of the spatio-temporal divisive normalization processor

Figure 4

Example of identification of a divisive normalization model. (a) $\mathcal{P}{h}_1^1$ (blue) and $\widehat{\mathcal{P}{h}_1^1}$ (red, SNR 60.56 [dB]), (b) $\mathcal{P}{h}_1^2$ (blue) and $\widehat{\mathcal{P}{h}_1^2}$ (red, SNR 60.48 [dB]), (c) $\mathcal{P}{h}_1^3$ (blue) and $\widehat{\mathcal{P}{h}_1^3}$ (red, SNR 49.56 [dB]), (d) $\mathcal{P}{h}_2^1$, (e) $\mathcal{P}{h}_2^2$, (f) $\mathcal{P}{h}_2^3$, (g) $\widehat{\mathcal{P}{h}_2^1}$ (SNR 60.59 [dB]), (h) $\widehat{\mathcal{P}{h}_2^2}$ (SNR 60.54 [dB]), (i) $\widehat{\mathcal{P}{h}_2^3}$ (SNR 60.61 [dB])

Figure 5

Output of the identified DNP model of the photoreceptor. (a) The stimulus presented to the photoreceptor; 5% of the stimulus was used for identification. (b) Comparison of the output of the detailed biophysical photoreceptor model (blue) with the output of the DNP model (red) and the output of the model without normalization, i.e., with ${\mathcal{T}}_1$ only (yellow)

Figure 6

Identified filters of the DNP model of the photoreceptor given in Example 2. (a) $\widehat{\mathcal{P}{h}_1^1}$, (b) $\widehat{\mathcal{P}{h}_1^2}$, (c) $\widehat{\mathcal{P}{h}_2^1}$, (d) $\widehat{\mathcal{P}{h}_2^2}$

Figure 7

Evaluation of the DNP model of the photoreceptor. (a) Gaussian noise stimulus with a bandwidth of 50 Hz. (b) Output of the photoreceptor model (blue) and of the identified DNP model (red, SNR 15.04 [dB]). The output of the identified model without normalization is shown in yellow (SNR 4.55 [dB])

Figure 8

Example of identification of the spatio-temporal DNP given in Example 3. (a)–(c) Identification of the first-order filters (a) $h_1^1$, (b) $h_1^2$, and (c) $h_1^{i4}$, $i=1,2,3,4$. (d) Identification of the second-order filters (from top to bottom) $h_2^{ij4}$ with $i\le j$ for $i=1,2,3,4$ and $j=1,2,3,4$

Figure 9

The spatio-temporal DNP model can exhibit adaptation to local luminance. A DNP with four photoreceptors and an amacrine cell (see Example 1 for details) is adapted to a background intensity level at the beginning of each trial. One of the photoreceptors is then provided a two-second long flash of light, while the inputs to the other photoreceptors are kept at the background level. The relationship between the steady state response of the photoreceptor and the light intensity of the flash is shown for each of the background levels

Figure 10

Steady State I/O visualization for the DNP considered in Example 1. (a) Input stimuli comprising bar gratings at various luminances and RMS contrasts. (b) Responses of the DNP without the MVP block. (c) Responses of the DNP with the MVP block

Figure 11

RMS contrast of the input images in Figure 10 are plotted against the RMS contrasts of the responses (a) without and (b) with the MVP block

Figure 12

Graphical visualization of the feedback processor of the DNP used in Example 6. The value of the feedback is obtained by a weighted sum of the outputs at each pixel of a $16\times 16$ block (only five pixels are shown in each direction) processed by a temporal Volterra operator (represented by a cylinder). Each weight is the value of a Gaussian function evaluated at the distance between the location of the pixel and the center of the block

Figure 13

Steady state I/O visualization of the spatio-temporal DNP for natural images. Top Row—Input images. Second Row—Input images visualized on a logarithmic scale. Third Row—Responses without the MVP block. Fourth Row—Responses with the MVP block. Left Column—Stimuli presented at low luminance, Middle Column—Medium luminance, Right Column—High luminance