A computationally efficient nonparametric approach for changepoint detection

Abstract

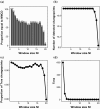
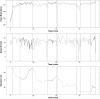
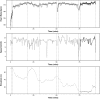
In this paper we build on an approach proposed by Zou et al. (2014) for nonparametric changepoint detection. This approach defines the best segmentation for a data set as the one which minimises a penalised cost function, with the cost function defined in term of minus a non-parametric log-likelihood for data within each segment. Minimising this cost function is possible using dynamic programming, but their algorithm had a computational cost that is cubic in the length of the data set. To speed up computation, Zou et al. (2014) resorted to a screening procedure which means that the estimated segmentation is no longer guaranteed to be the global minimum of the cost function. We show that the screening procedure adversely affects the accuracy of the changepoint detection method, and show how a faster dynamic programming algorithm, pruned exact linear time (PELT) (Killick et al. 2012), can be used to find the optimal segmentation with a computational cost that can be close to linear in the amount of data. PELT requires a penalty to avoid under/over-fitting the model which can have a detrimental effect on the quality of the detected changepoints. To overcome this issue we use a relatively new method, changepoints over a range of penalties (Haynes et al. 2016), which finds all of the optimal segmentations for multiple penalty values over a continuous range. We apply our method to detect changes in heart-rate during physical activity.

Keywords: Activity tracking; CROPS; Nonparametric maximum likelihood; PELT.

Fig. 1

a The number of replications out of 100 in which using NMCD+ with varying $N_I$ results in the same results as NMCD without screening. b The number of changepoints detected with with increasing window size $N_I$. c The proportion of true changepoints detected with varying window size $N_I$. d The computational time (s) for NMCD+ with increasing window size $N_I$

Fig. 2

a The proportion of true positive changepoints for a range of quantiles, K, in ED-PELT (solid) in comparison to ED-PELT (dashed). Black $n=100$, red $n=500$, blue: $n=1000$, grey $n=2000$ and dark green $n=5000$. b Relative speed of using ED-PELT compared to using ED-PELT. with varying number of quantiles, K. Black $n=100$, red $n=500$, blue $n=1000$ , grey $n=3000$, dark green $n=5000$ and purple n =10,000. (Color figure online)

Fig. 3

The cost vs number of changepoints plotted for a ED-PELT and b Change in slope. The red lines indicate the elbow and the blue circle highlights the point that we use as being the centre of the elbow. (Color figure online)

Fig. 4

Segmentations using ED-PELT with 10 changepoints. We have colour coded the line based on the average heart-rate of each segment where red peak, orange anaerobic, yellow aerobic and green recovery. (Color figure online)

Fig. 5

Segmentations using change in slope with 9 changepoints. We have colour coded the line based on the average heart-rate of each segment where red peak, orange anaerobic, yellow aerobic and green recovery. The solid black line in the top plot is the best fit for the mean within each segment. (Color figure online)