Review on Microbubbles and Microdroplets Flowing through Microfluidic Geometrical Elements

Abstract

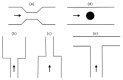
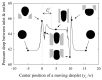
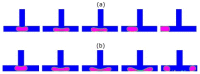
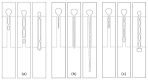
Two-phase flows are found in several industrial systems/applications, including boilers and condensers, which are used in power generation or refrigeration, steam generators, oil/gas extraction wells and refineries, flame stabilizers, safety valves, among many others. The structure of these flows is complex, and it is largely governed by the extent of interphase interactions. In the last two decades, due to a large development of microfabrication technologies, many microstructured devices involving several elements (constrictions, contractions, expansions, obstacles, or T-junctions) have been designed and manufactured. The pursuit for innovation in two-phase flows in these elements require an understanding and control of the behaviour of bubble/droplet flow. The need to systematize the most relevant studies that involve these issues constitutes the motivation for this review. In the present work, literature addressing gas-liquid and liquid-liquid flows, with Newtonian and non-Newtonian fluids, and covering theoretical, experimental, and numerical approaches, is reviewed. Particular focus is given to the deformation, coalescence, and breakup mechanisms when bubbles and droplets pass through the aforementioned microfluidic elements.

Keywords: T-junction; breakup; coalescence; constriction; contraction; deformation; microbubbles; microdroplets; microfluidic geometrical elements; two-phase flows.

Figure 1

Schematic representation of the most common microfluidic elements: (a) constriction; (b) expansion; (c) contraction; (d) obstacle; and, (e) T-junction.

Figure 2

Pressure drop in a constriction between inlet and outlet with $\mathsf{{\rm X}}=1$ and $\mathrm{Ca}=0.1$. $L_e^d$ is the entry length (i.e., the moving distance of the droplet since it enters the constriction until the pressure becomes constant), $w$ the constriction microchannel width, and $y_c$ the centre position of the moving droplet along the microchannel. Reproduced with permission from [46].

Figure 3

(a) droplet flow; (b) droplets contact; (c) squeezing; (d) fused droplet; (e) strongest deformation; and, (f) separated droplets. Reproduced with permission from [69].

Figure 4

Droplet shapes from two-dimensional (2D) numerical simulations with time progressing from left to right in a symmetric T-junction: (a) non-breaking droplet; and, (b) breaking droplet. Reproduced with permission from [15].

Figure 5

(i) Effect of the channel angle on bubble breakup: (a) 30°; (b) 90°; (c) 150°; (ii) Effect of the Capillary number, $\mathrm{Ca}$, on bubble breakup: (d) $\mathrm{Ca}=0.021$; (e) $\mathrm{Ca}=0.025$; (f) $\mathrm{Ca}=0.029$; (iii) Effect of the bubble length, $L$, on bubble breakup: (g) $L=1.03$ mm; (h) $L=1.24$ mm; and, (i) $L=1.42$ mm. Adapted with permission from [75].

Figure 6

Low-viscosity droplet deformation behaviour in constrictions for Newtonian fluids with X = 0.001: (a) Re = 2.13 × 10⁻³ and S = 2.13 × 10¹; (b) Re = 6.59 × 10⁻¹ and S = 3.97; and, (c) Re = 6.76 × 10⁻³ and S = 6.71. Adapted with permission from [80].

Figure 7

Droplet cross-section at the symmetric plane viewed from trop: (a) trap regime; (b) squeeze regime; and (c) breakup regime. $\mathrm{C}$ is a non-dimensional number representing the contraction level ($\mathrm{C}=D/W$, where $D$ is the droplet diameter, and $W$ the contraction microchannel width). In the thicker part of the microchannel (i.e., before the contraction), the inlet velocity is employed as the characteristic velocity, and the Capillary number is denoted as ${\mathrm{Ca}}_{\mathrm{I}}$, while the average velocity in the thinner region of the microchannel (i.e., after the contraction) is used to define the Capillary number ${\mathrm{Ca}}_{\mathrm{II}}$. Adapted with permission from [38].

Figure 8

Droplet passing through the obstacles: (a) single cylinder; (b) single square; and, (c) array of cylinders; (i) numerical results; (ii) experimental results. Adapted with permission from [92].