The Maximum Caliber Variational Principle for Nonequilibria
- PMID: 32075515
- PMCID: PMC9827727
- DOI: 10.1146/annurev-physchem-071119-040206
The Maximum Caliber Variational Principle for Nonequilibria
Abstract
Ever since Clausius in 1865 and Boltzmann in 1877, the concepts of entropy and of its maximization have been the foundations for predicting how material equilibria derive from microscopic properties. But, despite much work, there has been no equally satisfactory general variational principle for nonequilibrium situations. However, in 1980, a new avenue was opened by E.T. Jaynes and by Shore and Johnson. We review here maximum caliber, which is a maximum-entropy-like principle that can infer distributions of flows over pathways, given dynamical constraints. This approach is providing new insights, particularly into few-particle complex systems, such as gene circuits, protein conformational reaction coordinates, network traffic, bird flocking, cell motility, and neuronal firing.
Keywords: biological dynamics; caliber; entropy; inference; network models; nonequilibrium; variational principles.
Figures


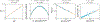
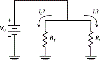

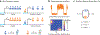

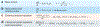
References
-
- Broder A. 2000. Graph structure in the web. Comput. Netw. 33:309–20
-
- Zipf GK. 1949. Human Behavior and the Principle of Least Effort. Cambridge, MA: Addison-Wesley
-
- Marsili M, Maslov S, Zhang YC. 1998. Dynamical optimization theory of a diversified portfolio. Phys. A Stat. Mech. Appl. 253:403–18

