The 2016 QSM Challenge: Lessons learned and considerations for a future challenge design

Abstract

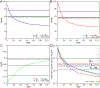
Purpose: The 4th International Workshop on MRI Phase Contrast and QSM (2016, Graz, Austria) hosted the first QSM Challenge. A single-orientation gradient recalled echo acquisition was provided, along with COSMOS and the χ₃₃ STI component as ground truths. The submitted solutions differed more than expected depending on the error metric used for optimization and were generally over-regularized. This raised (unanswered) questions about the ground truths and the metrics utilized.

Methods: We investigated the influence of background field remnants by applying additional filters. We also estimated the anisotropic contributions from the STI tensor to the apparent susceptibility to amend the χ₃₃ ground truth and to investigate the impact on the reconstructions. Lastly, we used forward simulations from the COSMOS reconstruction to investigate the impact noise had on the metric scores.

Results: Reconstructions compared against the amended STI ground truth returned lower errors. We show that the background field remnants had a minor impact in the errors. In the absence of inconsistencies, all metrics converged to the same regularization weights, whereas structural similarity index metric was more insensitive to such inconsistencies.

Conclusion: There was a mismatch between the provided data and the ground truths due to the presence of unaccounted anisotropic susceptibility contributions and noise. Given the lack of reliable ground truths when using in vivo acquisitions, simulations are suggested for future QSM Challenges.

Keywords: FANSI; magnetic susceptibility; quantitative susceptibility mapping; total variation.

Figure 1.

Single orientation acquisition (A) and background remnant models using (B) weak-harmonics (WH-QSM, with β=5, μ_h=0.1, the weak harmonic regularization weights) and (C) the Projection onto Dipole Fields (PDF) methods.

Figure 2.

Differences between forward simulated phases and the provided single orientation acquisition (A) for: (B and E) the χ₃₃ component, (C and F) COSMOS, and (D and G) the STI equation, including the χ₁₃ and χ₂₃ anisotropic components. The right column shows the same difference maps as the left column, but with a higher contrast to reveal subtle differences.

Figure 3.

The χ₃₃ (isotropic) component and correction factors, χ_corr (B and C, derived from χ₁₃ and χ₂₃ anisotropic components) used to estimate χ_STI-TKD and χ_STI-L2 respectively (D and E).

Figure 4.

Selected optimal reconstructions of the challenge data, based on the RMSE (left panel) and SSIM (right panel) metrics, using χ₃₃ (A,D) and χ_STI-L2 (B, E) as ground truth. (C ,F) show optimal reconstructions of the amended phase (to remove anisotropic components) and using χ₃₃ as ground truth (χ₃₃|Φ₃₃).

Figure 5.

Metric scores of the reconstruction using COSMOS-based forward simulations. Optimal (A) RMSE, (B) HFEN and (C) SSIM scores are presented as function of SNR. Metric scores for in vivo reconstructions using χ₃₃ and χ_STI-L2 as ground truth, along with reconstructions of the amended phase with TV-FANSI (χ₃₃|Φ₃₃) and WH-QSM, are also included. (D) presents the optimal regularization weight for each metric and SNR setting. Ranges for the optimal reconstructions using χ₃₃, χ_STI-L2 and χ₃₃|Φ₃₃ also included.

Figure 6.

(A) RMSE, (B) HFEN and (C) SSIM optimal scores for reconstructions at SNR=64 and SNR=32 and their regularization weight. Simulations included the phase forward calculated using COSMOS Φ with the addition of the background remnants obtained using PDF (Φ_PDF) and the anisotropic phase contributions (Φ_corr) calculated from the χ₁₃ and χ₂₃ components of the STI tensor. (D) Shows the range span of optimal regularization weight values by the different simulations and in vivo reconstructions, for a given metric.