A tutorial on sample size calculation for multiple-period cluster randomized parallel, cross-over and stepped-wedge trials using the Shiny CRT Calculator
- PMID: 32087011
- PMCID: PMC7394950
- DOI: 10.1093/ije/dyz237
A tutorial on sample size calculation for multiple-period cluster randomized parallel, cross-over and stepped-wedge trials using the Shiny CRT Calculator
Abstract
It has long been recognized that sample size calculations for cluster randomized trials require consideration of the correlation between multiple observations within the same cluster. When measurements are taken at anything other than a single point in time, these correlations depend not only on the cluster but also on the time separation between measurements and additionally, on whether different participants (cross-sectional designs) or the same participants (cohort designs) are repeatedly measured. This is particularly relevant in trials with multiple periods of measurement, such as the cluster cross-over and stepped-wedge designs, but also to some degree in parallel designs. Several papers describing sample size methodology for these designs have been published, but this methodology might not be accessible to all researchers. In this article we provide a tutorial on sample size calculation for cluster randomized designs with particular emphasis on designs with multiple periods of measurement and provide a web-based tool, the Shiny CRT Calculator, to allow researchers to easily conduct these sample size calculations. We consider both cross-sectional and cohort designs and allow for a variety of assumed within-cluster correlation structures. We consider cluster heterogeneity in treatment effects (for designs where treatment is crossed with cluster), as well as individually randomized group-treatment trials with differential clustering between arms, for example designs where clustering arises from interventions being delivered in groups. The calculator will compute power or precision, as a function of cluster size or number of clusters, for a wide variety of designs and correlation structures. We illustrate the methodology and the flexibility of the Shiny CRT Calculator using a range of examples.
© The Author(s) 2020. Published by Oxford University Press on behalf of the International Epidemiological Association.
Figures

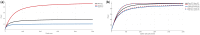
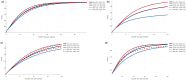
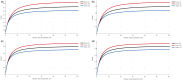
References
-
- Eldridge S, Kerry S.. A Practical Guide to Cluster Randomized Trials in Health Services Research. Chichester, UK: Wiley, 2012.
-
- Hayes RJ, Bennett S.. Simple sample size calculation for cluster-randomized trials. Int J Epidemiol 1999;28:319–26. - PubMed
-
- Teerenstra S, Eldridge S, Graff M, de Hoop E, Borm GF.. A simple sample size formula for analysis of covariance in cluster randomized trials. Stat Med 2012;31:2169–78. - PubMed
-
- Hooper R, Forbes A, Hemming K, Takeda A, Beresford L.. Analysis of cluster randomized trials with an assessment of outcome at baseline. BMJ 2018;360:k1121. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Medical
Research Materials

