Image Reconstruction: From Sparsity to Data-adaptive Methods and Machine Learning
- PMID: 32095024
- PMCID: PMC7039447
- DOI: 10.1109/JPROC.2019.2936204
Image Reconstruction: From Sparsity to Data-adaptive Methods and Machine Learning
Abstract
The field of medical image reconstruction has seen roughly four types of methods. The first type tended to be analytical methods, such as filtered back-projection (FBP) for X-ray computed tomography (CT) and the inverse Fourier transform for magnetic resonance imaging (MRI), based on simple mathematical models for the imaging systems. These methods are typically fast, but have suboptimal properties such as poor resolution-noise trade-off for CT. A second type is iterative reconstruction methods based on more complete models for the imaging system physics and, where appropriate, models for the sensor statistics. These iterative methods improved image quality by reducing noise and artifacts. The FDA-approved methods among these have been based on relatively simple regularization models. A third type of methods has been designed to accommodate modified data acquisition methods, such as reduced sampling in MRI and CT to reduce scan time or radiation dose. These methods typically involve mathematical image models involving assumptions such as sparsity or low-rank. A fourth type of methods replaces mathematically designed models of signals and systems with data-driven or adaptive models inspired by the field of machine learning. This paper focuses on the two most recent trends in medical image reconstruction: methods based on sparsity or low-rank models, and data-driven methods based on machine learning techniques.
Keywords: Compressed sensing; Deep learning; Dictionary learning; Efficient algorithms; Image reconstruction; MRI; Machine learning; Multi-layer models; Nonconvex optimization; PET; SPECT; Sparse and low-rank models; Structured models; Transform learning; X-ray CT.
Figures

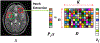
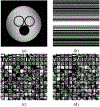

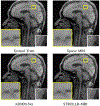
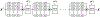
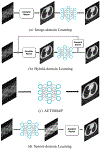
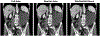


Similar articles
-
Radiation dose reduction in medical x-ray CT via Fourier-based iterative reconstruction.Med Phys. 2013 Mar;40(3):031914. doi: 10.1118/1.4791644. Med Phys. 2013. PMID: 23464329 Free PMC article.
-
LRR-CED: low-resolution reconstruction-aware convolutional encoder-decoder network for direct sparse-view CT image reconstruction.Phys Med Biol. 2022 Jul 19;67(15). doi: 10.1088/1361-6560/ac7bce. Phys Med Biol. 2022. PMID: 35738249
-
Low-dose CT reconstruction via L1 dictionary learning regularization using iteratively reweighted least-squares.Biomed Eng Online. 2016 Jun 18;15(1):66. doi: 10.1186/s12938-016-0193-y. Biomed Eng Online. 2016. PMID: 27316680 Free PMC article.
-
Image reconstruction: Part 1 - understanding filtered back projection, noise and image acquisition.J Cardiovasc Comput Tomogr. 2020 May-Jun;14(3):219-225. doi: 10.1016/j.jcct.2019.04.008. Epub 2019 Apr 16. J Cardiovasc Comput Tomogr. 2020. PMID: 31023632 Review.
-
Basics of iterative reconstruction methods in computed tomography: A vendor-independent overview.Eur J Radiol. 2018 Dec;109:147-154. doi: 10.1016/j.ejrad.2018.10.025. Epub 2018 Oct 26. Eur J Radiol. 2018. PMID: 30527298 Review.
Cited by
-
Boosting the signal-to-noise of low-field MRI with deep learning image reconstruction.Sci Rep. 2021 Apr 15;11(1):8248. doi: 10.1038/s41598-021-87482-7. Sci Rep. 2021. PMID: 33859218 Free PMC article.
-
UNCERTAINTY-GUIDED PHYSICS-DRIVEN DEEP LEARNING RECONSTRUCTION VIA CYCLIC MEASUREMENT CONSISTENCY.Proc IEEE Int Conf Acoust Speech Signal Process. 2024 Apr;2024:13441-13445. doi: 10.1109/icassp48485.2024.10447594. Epub 2024 Mar 18. Proc IEEE Int Conf Acoust Speech Signal Process. 2024. PMID: 39829965 Free PMC article.
-
Inpainted Image Reconstruction Using an Extended Hopfield Neural Network Based Machine Learning System.Sensors (Basel). 2022 Jan 21;22(3):813. doi: 10.3390/s22030813. Sensors (Basel). 2022. PMID: 35161559 Free PMC article.
-
A cone-beam X-ray computed tomography data collection designed for machine learning.Sci Data. 2019 Oct 22;6(1):215. doi: 10.1038/s41597-019-0235-y. Sci Data. 2019. PMID: 31641152 Free PMC article.
-
Implicit data crimes: Machine learning bias arising from misuse of public data.Proc Natl Acad Sci U S A. 2022 Mar 29;119(13):e2117203119. doi: 10.1073/pnas.2117203119. Epub 2022 Mar 21. Proc Natl Acad Sci U S A. 2022. PMID: 35312366 Free PMC article.
References
-
- Feldkamp LA, Davis LC, and Kress JW, “Practical cone beam algorithm,” J. Opt. Soc. Am. A, vol. 1, pp. 612–9, June 1984.
-
- Fessler JA and Sutton BP, “Nonuniform fast Fourier transforms using min-max interpolation,” IEEE Trans. Sig. Proc, vol. 51, pp. 560–74, February 2003.
-
- De Francesco S and Ferreira da Silva AM, “Efficient NUFFT-based direct Fourier algorithm for fan beam CT reconstruction,” in Proc. SPIE 5370 Medical Imaging: Image Proc., pp. 666–77, 2004.
-
- Sauer K and Bouman C, “A local update strategy for iterative reconstruction from projections,” IEEE Trans. Sig. Proc, vol. 41, pp. 534–48, February 1993.
-
- Thibault J-B, Bouman CA, Sauer KD, and Hsieh J, “A recursive filter for noise reduction in statistical iterative tomographic imaging,” in Proc. SPIE 6065 Computational Imaging IV, p. 60650X, 2006.
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Miscellaneous
