Relative Efficiencies of Simple and Complex Substitution Models in Estimating Divergence Times in Phylogenomics
- PMID: 32119075
- PMCID: PMC7253201
- DOI: 10.1093/molbev/msaa049
Relative Efficiencies of Simple and Complex Substitution Models in Estimating Divergence Times in Phylogenomics
Abstract
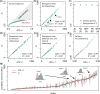
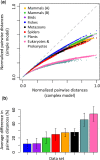
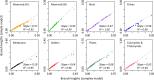
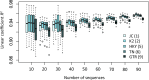
The conventional wisdom in molecular evolution is to apply parameter-rich models of nucleotide and amino acid substitutions for estimating divergence times. However, the actual extent of the difference between time estimates produced by highly complex models compared with those from simple models is yet to be quantified for contemporary data sets that frequently contain sequences from many species and genes. In a reanalysis of many large multispecies alignments from diverse groups of taxa, we found that the use of the simplest models can produce divergence time estimates and credibility intervals similar to those obtained from the complex models applied in the original studies. This result is surprising because the use of simple models underestimates sequence divergence for all the data sets analyzed. We found three fundamental reasons for the observed robustness of time estimates to model complexity in many practical data sets. First, the estimates of branch lengths and node-to-tip distances under the simplest model show an approximately linear relationship with those produced by using the most complex models applied on data sets with many sequences. Second, relaxed clock methods automatically adjust rates on branches that experience considerable underestimation of sequence divergences, resulting in time estimates that are similar to those from complex models. And, third, the inclusion of even a few good calibrations in an analysis can reduce the difference in time estimates from simple and complex models. The robustness of time estimates to model complexity in these empirical data analyses is encouraging, because all phylogenomics studies use statistical models that are oversimplified descriptions of actual evolutionary substitution processes.
Keywords: RelTime; molecular dating; phylogenomics; relaxed clock; substitution model.
© The Author(s) 2020. Published by Oxford University Press on behalf of the Society for Molecular Biology and Evolution.
Figures




Similar articles
-
Assessing Rapid Relaxed-Clock Methods for Phylogenomic Dating.Genome Biol Evol. 2021 Nov 5;13(11):evab251. doi: 10.1093/gbe/evab251. Genome Biol Evol. 2021. PMID: 34751377 Free PMC article.
-
Characterization of the uncertainty of divergence time estimation under relaxed molecular clock models using multiple loci.Syst Biol. 2015 Mar;64(2):267-80. doi: 10.1093/sysbio/syu109. Epub 2014 Dec 11. Syst Biol. 2015. PMID: 25503979 Free PMC article.
-
Performance of relaxed-clock methods in estimating evolutionary divergence times and their credibility intervals.Mol Biol Evol. 2010 Jun;27(6):1289-300. doi: 10.1093/molbev/msq014. Epub 2010 Jan 21. Mol Biol Evol. 2010. PMID: 20093431 Free PMC article.
-
Implementing and testing the multispecies coalescent model: A valuable paradigm for phylogenomics.Mol Phylogenet Evol. 2016 Jan;94(Pt A):447-62. doi: 10.1016/j.ympev.2015.10.027. Epub 2015 Oct 27. Mol Phylogenet Evol. 2016. PMID: 26518740 Review.
-
[Molecular dating in the genomic era].Med Sci (Paris). 2006 Apr;22(4):374-80. doi: 10.1051/medsci/2006224374. Med Sci (Paris). 2006. PMID: 16597406 Review. French.
Cited by
-
Consequences of Substitution Model Selection on Protein Ancestral Sequence Reconstruction.Mol Biol Evol. 2022 Jul 2;39(7):msac144. doi: 10.1093/molbev/msac144. Mol Biol Evol. 2022. PMID: 35789388 Free PMC article.
-
Extant Sequence Reconstruction: The Accuracy of Ancestral Sequence Reconstructions Evaluated by Extant Sequence Cross-Validation.J Mol Evol. 2024 Apr;92(2):181-206. doi: 10.1007/s00239-024-10162-3. Epub 2024 Mar 19. J Mol Evol. 2024. PMID: 38502220 Free PMC article.
-
Ancestral sequence reconstruction as a tool to study the evolution of wood decaying fungi.Front Fungal Biol. 2022 Oct 14;3:1003489. doi: 10.3389/ffunb.2022.1003489. eCollection 2022. Front Fungal Biol. 2022. PMID: 37746217 Free PMC article. Review.
-
Assessing the relative performance of fast molecular dating methods for phylogenomic data.BMC Genomics. 2022 Dec 3;23(1):798. doi: 10.1186/s12864-022-09030-5. BMC Genomics. 2022. PMID: 36460948 Free PMC article.
-
Challenges in Assembling the Dated Tree of Life.Genome Biol Evol. 2024 Oct 9;16(10):evae229. doi: 10.1093/gbe/evae229. Genome Biol Evol. 2024. PMID: 39475308 Free PMC article.
References
-
- Alfaro ME, Faircloth BC, Harrington RC, Sorenson L, Friedman M, Thacker CE, Oliveros CH, Černý D, Near TJ.. 2018. Explosive diversification of marine fishes at the Cretaceous-Palaeogene boundary. Nat Ecol Evol. 2(4):688–696. - PubMed
-
- Alfaro ME, Holder MT.. 2006. The posterior and the prior in Bayesian phylogenetics. Annu Rev Ecol Evol Syst. 37(1):19–42.
-
- Arbogast BS, Edwards SV, Wakeley J, Beerli P, Slowinski JB.. 2002. Estimating divergence times from molecular data on phylogenetic and population genetic timescales. Annu Rev Ecol Syst. 33(1):707–740.
Publication types
MeSH terms
Associated data
Grants and funding
LinkOut - more resources
Full Text Sources

