A multilayer temporal network model for STD spreading accounting for permanent and casual partners

Abstract

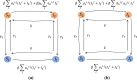
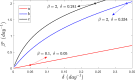
Sexually transmitted diseases (STD) modeling has used contact networks to study the spreading of pathogens. Recent findings have stressed the increasing role of casual partners, often enabled by online dating applications. We study the Susceptible-Infected-Susceptible (SIS) epidemic model -appropriate for STDs- over a two-layer network aimed to account for the effect of casual partners in the spreading of STDs. In this novel model, individuals have a set of steady partnerships (links in layer 1). At certain rates, every individual can switch between active and inactive states and, while active, it establishes casual partnerships with some probability with active neighbors in layer 2 (whose links can be thought as potential casual partnerships). Individuals that are not engaged in casual partnerships are classified as inactive, and the transitions between active and inactive states are independent of their infectious state. We use mean-field equations as well as stochastic simulations to derive the epidemic threshold, which decreases substantially with the addition of the second layer. Interestingly, for a given expected number of casual partnerships, which depends on the probabilities of being active, this threshold turns out to depend on the duration of casual partnerships: the longer they are, the lower the threshold.

Figure 1

A snapshot from a realization of the network model. At any time t the nodes are either active or inactive. A potential link is activated with probability p₀ if its both ends are active at the same time.

Figure 2

The figures show the diagrams of node transitions among different node states. The rate of each transition is specified on the arrow that indicates the transition. (a) shows diagram of the Markov process which is discussed in section 2.2, and (b) shows diagram of the exact process. In these figures $I_1^j=1$ ($I_2^j=1$) if node j is infected and inactive (active), otherwise it is zero. In diagram (b) $X_0^{i,j}$ is a Bernoulli random variable that has value one with probability p₀. This random variable is drawn each time a pair of active nodes (i, j) with a potential link between them occurs, regardless of their disease status.

Figure 3

Critical value of β as a function of γ₁ in regular random networks. Parameters: k₁ = 4, k₂ = 50, p₀ = 0.1, δ = 1, γ₂ = γ₁ (p₂ = 0.5).

Figure 4

Disease prevalence as a function of p₂ in regular random networks. Circles show, for each set of parameters values, the median of the prevalence in networks of size 500 after 1000 runs of the Markov process approximated by the mean-field model, and error bars show the corresponding interquartile range. Parameters: k₁ = 4, k₂ = 50, p₀ = 0.5, β = 0.2, δ = 1, γ₁ = 0.01 (red), γ₁ = 10 (black).

Figure 5

Results of numerical and stochastic simulations of the spreading processes on random regular graphs, discussed in section 4. Panel (a) shows the comparison of different approximate processes with the exact process; panel (b) shows the epidemic threshold of the exact process, as a function of p₂ (probability of being active in ${\mathbb{L}}_2$) and the parameter γ₂, which is proportional to the inverse of expected duration of active potential links; panel (c) shows how the infection prevalence in the metastable state is affected by different parameters in the exact process. Error bars show the median and the interquartile range.

Figure 6

Infection transmission rate threshold as a function of recovery rate for three different temporal networks discussed in section 4. Case a corresponds to partnerships of 60 days duration and cases b,c correspond to casual sexual encounters.