Stochastic Model of T Cell Repolarization during Target Elimination I

Abstract

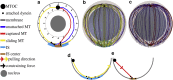
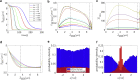
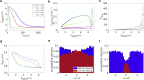
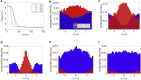
Cytotoxic T lymphocytes (T) and natural killer cells are the main cytotoxic killer cells of the human body to eliminate pathogen-infected or tumorigenic cells (i.e., target cells). Once a natural killer or T cell has identified a target cell, they form a tight contact zone, the immunological synapse (IS). One then observes a repolarization of the cell involving the rotation of the microtubule (MT) cytoskeleton and a movement of the MT organizing center (MTOC) to a position that is just underneath the plasma membrane at the center of the IS. Concomitantly, a massive relocation of organelles attached to MTs is observed, including the Golgi apparatus, lytic granules, and mitochondria. Because the mechanism of this relocation is still elusive, we devise a theoretical model for the molecular-motor-driven motion of the MT cytoskeleton confined between plasma membrane and nucleus during T cell polarization. We analyze different scenarios currently discussed in the literature, the cortical sliding and capture-shrinkage mechanisms, and compare quantitative predictions about the spatiotemporal evolution of MTOC position and MT cytoskeleton morphology with experimental observations. The model predicts the experimentally observed biphasic nature of the repositioning due to an interplay between MT cytoskeleton geometry and motor forces and confirms the dominance of the capture-shrinkage over the cortical sliding mechanism when the MTOC and IS are initially diametrically opposed. We also find that the two mechanisms act synergistically, thereby reducing the resources necessary for repositioning. Moreover, it turns out that the localization of dyneins in the peripheral supramolecular activation cluster facilitates their interaction with the MTs. Our model also opens a way to infer details of the dynein distribution from the experimentally observed features of the MT cytoskeleton dynamics. In a subsequent publication, we will address the issue of general initial configurations and situations in which the T cell established two ISs.

Figure 1

(a–c) Sketch of the model. (a) A two-dimensional cross-section of the model is shown. MTs sprout from the MTOC, and their movement is confined by constraining forces from the cell membrane and the nucleus. MTs are attached to dynein motors in the IS, and they are pulled by the capture-shrinkage or the cortical sliding mechanism. (b and c) A three-dimensional sketch of the cell model is given. The outer transparent and inner spheres represent the cell membrane and the nucleus of the cell, respectively. (b) The blue disk represents the IS, where cortical sliding dynein is anchored. Small green dots in the IS represent randomly distributed dynein. (c) The brown disk represents the central region of the IS where the capture-shrinkage dynein is anchored. (d and e) A sketch of the cortical sliding mechanism (d) and the capture-shrinkage mechanism (e) is shown. Small black dots on the membrane: dynein anchor points, small black dots on the MTs: attachment points. Note that MTs depolymerize when pulled by capture-shrinkage dynein toward the membrane. To see this figure in color, go online.

Figure 2

Snapshots from the time evolution of the MT cytoskeleton configuration under the effect of the capture-shrinkage mechanism alone (dynein density ρ_IS = 100 μm⁻²). MTs are connected to the MTOC indicated by the large black sphere. Blue and red curves are unattached and attached MTs. Small black spheres in the IS represent dyneins. The brown cylinder indicates the center of the IS, where the capture-shrinkage dyneins are located. (a and d) d_MIS = 9 μm. Initially, the attached MTs sprout from the MTOC in all directions. (b and e) d_MIS = 6 μm. As time progresses, MTs form a stalk connecting the MTOC and the IS. (c and f) d_MIS = 2.5 μm. The stalk is fully formed, and it shortens as the MTOC approaches the IS. To see this figure in color, go online.

Figure 3

Capture-shrinkage mechanism: (a) the dependence of the average MTOC-IS distance ${\overline{d}}_{\text{MIS}}$ on time. The error bars are represented by dashed lines and are plotted only if bigger than a symbol size. (b–d) Dependencies of the average MTOC velocity ${\overline{v}}_{\text{MTOC}}$ (b), the number of dyneins acting on microtubules ${\overline{N}}_{\text{dm}}$ (c), and the MTOC-center distance ${\overline{d}}_{\text{MC}}$ (d) on the average MTOC-IS distance are shown. Black dashed lines denote transitions between different phases of the repositioning process. (e and f) Probability distributions of the angles between the first MT segments and the direction of the MTOC movement for a dynein density ρ_IS = 100 μm⁻² (e), t = 1 s, ${\overline{d}}_{\text{MIS}}$ ∼ 9 μm are given. (f) t = 60 s, ${\overline{d}}_{\text{MIS}}$ ∼ 5 μm. To see this figure in color, go online.

Figure 4

Snapshots from the time evolution of the MT cytoskeleton configuration under the effect of cortical sliding mechanism with a low dynein density, ${\tilde{\rho }}_{\text{IS}}$ = 60 μm⁻². The cyan cylinder indicates the IS area. Blue and yellow lines are unattached and attached MTs, respectively. The black spheres in the IS are the positions of dyneins attached to MTs. (a and d) ${\overline{d}}_{\text{MIS}}$ = 9 μm. Originally, the attached MTs aim from the MTOC in every direction. (b and e) ${\overline{d}}_{\text{MIS}}$ = 4.5 μm. MTs attached to dynein aim predominantly in one direction. (c and f) ${\overline{d}}_{\text{MIS}}$ = 1.5 μm. Just a few MTs remain under the actions of cortical sliding, and they rarely touch the surface of the cell in the IS. To see this figure in color, go online.

Figure 5

Cortical sliding with low dynein densities ${\tilde{\rho }}_{\text{IS}}$. (a) The dependence of the average MTOC-IS distance ${\overline{d}}_{\text{MIS}}$ on time is shown. The error bars are represented by dashed lines and are plotted only if bigger than a symbol size. (b–d) Dependencies of the average MTOC velocity ${\overline{v}}_{\text{MTOC}}$ (b), number of dyneins acting on MTs ${\overline{N}}_{\text{dm}}$ (c), and the MTOC-center distance ${\overline{d}}_{\text{MC}}$ (d) on the average MTOC-IS distance are shown. (e and f) Probability distributions of the angles α between the first MT segment and the MTOC motion, ${\tilde{\rho }}_{\text{IS}}$ = 60 μm⁻², are shown. (e) t = 5 s, ${\overline{d}}_{\text{MIS}}$ ∼ 9 μm. (f) t = 65 s, ${\overline{d}}_{\text{MIS}}$ ∼ 5 μm. To see this figure in color, go online.

Figure 6

Snapshots from the time evolution of the MT cytoskeleton configuration under the effect of cortical sliding alone, with a medium area density of the dynein ${\tilde{\rho }}_{\text{IS}}$ = 200 μm⁻²) from two perspectives. (a and c) ${\overline{d}}_{\text{MIS}}$ = 9 μm. MTs sprout from the MTOC in all directions. (b and d) ${\overline{d}}_{\text{MIS}}$ = 5 μm. The majority of MTs are attached, and the MT cytoskeleton is deformed. (c and e) ${\overline{d}}_{\text{MIS}}$ = 1 μm. At the end of the repositioning, the MTOC passed the center of the IS, and attached MTs aim in all directions. To see this figure in color, go online.

Figure 7

Cortical sliding mechanism with medium dynein densities ${\tilde{\rho }}_{\text{IS}}$. (a) The dependence of the MTOC-IS distance ${\overline{d}}_{\text{MIS}}$ on time is shown. Probability distributions of the angles α between the first MT segment and the MTOC motion, ${\tilde{\rho }}_{\text{IS}}$ = 200 μm⁻², are shown. (b) t = 5 s, ${\overline{d}}_{\text{MIS}}$ ∼ 9 μm. (c) t = 15 s, ${\overline{d}}_{\text{MIS}}$ ∼ 6 μm. (d) t = 20 s, ${\overline{d}}_{\text{MIS}}$ ∼ 2.5 μm. (e) t = 25 s, ${\overline{d}}_{\text{MIS}}$ ∼ 1.5 μm, other side of IS. (f) t = 60 s, ${\overline{d}}_{\text{MIS}}$ ∼ 0.8 μm. To see this figure in color, go online.

Figure 8

Cortical sliding with high dynein densities ${\tilde{\rho }}_{\text{IS}}$. (a) The dependence of the average MTOC-IS distance ${\overline{d}}_{\text{MIS}}$ on time is shown. The error bars are represented by dashed lines and are plotted only if bigger than a symbol size. (b) The dependence of the average number of dyneins ${\overline{N}}_{\text{dm}}$ on the MTOC-IS distance is shown. (c) Probability distribution of the angle α between the first MT segment of attached MTs and the direction of the MTOC motion, ${\overline{d}}_{\text{MIS}}$ ∼ 5 μm, is shown. (d) The probability distribution of the distance of attached dynein anchor points from the axis of the IS r_IS when ${\overline{d}}_{\text{MIS}}$ ∼ 5 μm is shown. (e and f) The two-dimensional probability density of attached dyneins in the IS, ${\overline{d}}_{\text{MIS}}$ = 5 μm, is shown. (e) Area density of cortical sliding dyneins ${\tilde{\rho }}_{\text{IS}}$ = 500 μm⁻². (f) ${\tilde{\rho }}_{\text{IS}}$ = 1000 μm⁻². To see this figure in color, go online.

Figure 9

Comparison of the capture-shrinkage and the cortical sliding mechanisms in terms of the average MTOC velocity in both phases ${\overline{V}}_{\text{MTOC}}$, times of repositioning, and the final MTOC-IS distance ${\overline{d}}_{\text{MIS}}$. (a) The MTOC velocity in the first and the second phase is shown. (b) Repositioning times are shown. Final MTOC-IS distances are shown in the inset. (c) The dependence of the average distance ${\overline{r}}_{\text{IS}}$ of attached dynein motors from the axis of the IS on dynein area density ${\tilde{\rho }}_{\text{IS}}$ for the case of sole cortical sliding is shown. The error bars are represented by dashed lines and are plotted only if bigger than a symbol size. To see this figure in color, go online.

Figure 10

Combination of capture-shrinkage and cortical sliding: (a) dependence of the average MTOC-IS distance ${\overline{d}}_{\text{MIS}}$ on time. Dependence of the average MTOC velocity ${\overline{v}}_{\text{MTOC}}$ (b), the average number of attached capture-shrinkage dyneins ${\overline{N}}_{\text{capt}}$ (c), and the average number of attached cortical sliding dyneins ${\overline{N}}_{\text{cort}}$ (d) on the average MTOC-IS distance is shown (cortical sliding densities corresponding to different line colors in b–d are the same as in a). (e) The probability density of the angles α between the first MT segment and the direction of the MTOC motion is shown; t = 50 s, ${\overline{d}}_{\text{MIS}}$ ∼ 5 μm, ${\tilde{\rho }}_{\text{IS}}$ = ρ_IS = 60 μm⁻². (f) Dependence of times of repositioning on cortical sliding area density ${\tilde{\rho }}_{\text{IS}}$ is shown. The error bars are represented by dashed lines and are plotted only if bigger than a symbol size. To see this figure in color, go online.

Figure 11

Combination of capture-shrinkage and cortical sliding. (a) Dependence of the average distance between the center of the cell and the MTOC ${\overline{d}}_{\text{MC}}$ on the average MTOC-IS distance ${\overline{d}}_{\text{MIS}}$ is shown. (b and c) A probability density plot for the spatial distribution of attached dynein is given. (b) t = 50 s, ${\overline{d}}_{\text{MIS}}$ ∼ 4.5 μm. (c) t = 60 s, ${\overline{d}}_{\text{MIS}}$ ∼ 1.5 μm. (d) Repositioning times as a function of the density of capture-shrinkage dynein ρ_IS for four different values of the cortical sliding area density ${\tilde{\rho }}_{\text{IS}}$ are shown. The error bars are represented by dashed lines and are plotted only if bigger than a symbol size. (e–g) Snapshots from simulation are given. The blue, red, and bold yellow curves correspond to MTs without dynein and with capture-shrinkage and cortical sliding, respectively. Black dots depict positions of attached dynein motors. (e) d_MIS = 4.5 μm, (f) d_MIS = 2.5 μm, and (g) d_MIS = 1 μm. To see this figure in color, go online.