Networks and long-range mobility in cities: A study of more than one billion taxi trips in New York City
- PMID: 32132592
- PMCID: PMC7055277
- DOI: 10.1038/s41598-020-60875-w
Networks and long-range mobility in cities: A study of more than one billion taxi trips in New York City
Abstract
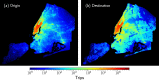
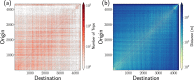
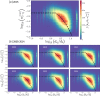
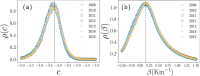
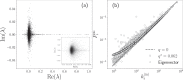
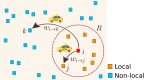
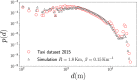
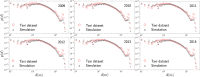
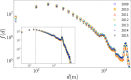
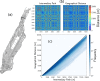
We analyze the massive data set of more than one billion taxi trips in New York City, from January 2009 to December 2015. With these records of seven years, we generate an origin-destination matrix that has information of a vast number of trips. The mobility and flow of taxis can be described as a directed weighted network that connects different zones of high demand for taxis. This network has in and out degrees that follow a stretched exponential and a power law with an exponential cutoff distributions, respectively. Using the origin-destination matrix, we obtain a rank, called "OD rank", analogous to the page rank of Google, that gives the more relevant places in New York City in terms of taxi trips. We introduced a model that captures the local and global dynamics that agrees with the data. Considering the taxi trips as a proxy of human mobility in cities, it might be possible that the long-range mobility found for New York City would be a general feature in other large cities around the world.
Conflict of interest statement
The authors declare no competing interests.
Figures


Similar articles
-
Visual exploration of big spatio-temporal urban data: a study of New York City taxi trips.IEEE Trans Vis Comput Graph. 2013 Dec;19(12):2149-58. doi: 10.1109/TVCG.2013.226. IEEE Trans Vis Comput Graph. 2013. PMID: 24051781
-
Exploring spatio-temporal impact of COVID-19 on citywide taxi demand: A case study of New York City.PLoS One. 2024 Apr 16;19(4):e0299093. doi: 10.1371/journal.pone.0299093. eCollection 2024. PLoS One. 2024. PMID: 38626168 Free PMC article.
-
Revealing latent characteristics of mobility networks with coarse-graining.Sci Rep. 2019 May 17;9(1):7545. doi: 10.1038/s41598-019-44005-9. Sci Rep. 2019. PMID: 31101843 Free PMC article.
-
Impact of COVID-19 on the mobility patterns: An investigation of taxi trips in Chicago.PLoS One. 2022 May 5;17(5):e0267436. doi: 10.1371/journal.pone.0267436. eCollection 2022. PLoS One. 2022. PMID: 35511884 Free PMC article.
-
Impact of the mixed degree of urban functions on the taxi travel demand.PLoS One. 2021 Mar 4;16(3):e0247431. doi: 10.1371/journal.pone.0247431. eCollection 2021. PLoS One. 2021. PMID: 33661952 Free PMC article. Review.
Cited by
-
Activity of vehicles in the bus rapid transit system Metrobús in Mexico City.Sci Rep. 2022 Jan 7;12(1):98. doi: 10.1038/s41598-021-04037-6. Sci Rep. 2022. PMID: 34997045 Free PMC article.
-
Intermunicipal travel networks of Mexico during the COVID-19 pandemic.Sci Rep. 2023 May 26;13(1):8566. doi: 10.1038/s41598-023-35542-5. Sci Rep. 2023. PMID: 37237051 Free PMC article.
-
Pattern detection in the vehicular activity of bus rapid transit systems.PLoS One. 2024 Oct 29;19(10):e0312541. doi: 10.1371/journal.pone.0312541. eCollection 2024. PLoS One. 2024. PMID: 39471165 Free PMC article.
-
A long-term travel delay measurement study based on multi-modal human mobility data.Sci Rep. 2022 Sep 26;12(1):15988. doi: 10.1038/s41598-022-19394-z. Sci Rep. 2022. PMID: 36163340 Free PMC article.
-
Public transport across models and scales: A case study of the Munich network.PNAS Nexus. 2024 Oct 31;3(11):pgae489. doi: 10.1093/pnasnexus/pgae489. eCollection 2024 Nov. PNAS Nexus. 2024. PMID: 39554514 Free PMC article.
References
-
- Batty, M. The New Science of Cities (MIT Press, Cambridge, MA, 2013).
-
- Barthélemy, M. The Structure and Dynamics of Cities: Urban Data Analysis and Theoretical Modeling (Cambridge University Press, 2016).
-
- Barbosa H, et al. Human mobility: Models and applications. Phys. Rep. 2018;734:1–74. doi: 10.1016/j.physrep.2018.01.001. - DOI
Publication types
LinkOut - more resources
Full Text Sources

