New Insights into Modelling Bacterial Growth with Reference to the Fish Pathogen Flavobacterium psychrophilum

Abstract

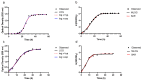
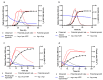
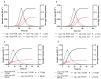
Two new models, based upon the principles promulgated by Baranyi and co-workers are presented and resulting growth functions evaluated based upon their ability to mimic bacterial growth of the fish pathogen Flavobacterium psychrophilum. These growth functions make use of a dampening function to suppress potential growth, represented by a logistic, and are derived from rate:state differential equations. Dampening effects are represented by a rectangular hyperbola or a simple exponential, incorporated into a logistic differential equation and solved analytically resulting in two newly derived growth equations, viz. logistic × hyperbola (log × hyp) and logistic × exponential (log × exp). These characteristics result in flexible and robust growth functions that can be expressed as equations with biologically meaningful parameters. The newly derived functions (log × hyp and log × exp), along with the Baranyi (BAR), simple logistic (LOG) and its modified form (MLOG) were evaluated based upon examination of residuals and measures of goodness-of-fit and cross-validation. Using these criteria, log × hyp, log × exp and BAR performed better than, or at least equally well as, LOG and MLOG. In contrast with log × exp and BAR, log × hyp can be easily manipulated mathematically allowing for simple algebraic expressions for time and microbial biomass at inflexion point, in addition to maximum and scaled maximum growth rates.

Keywords: Flavobacterium psychrophilum; bacterial diseases; farmed fish; modelling.

Figure 1

Optical density growth data and model predictions for Flavobacterium psychrophilum. Growth predictions using (a) LOG, log × hyp, log × exp and (b) MLOG and BAR, grown on a TYES liquid medium, and (c) LOG, log × hyp, log × exp and (d) MLOG and BAR, grown on a FLBP liquid medium. In panels (a) and (c), models are fitted to untransformed optical density measurements (OD) while (b) and (d) models are fitted to [ln(OD/OD₀)].

Figure 2

The effect of dampening potential growth rate, resulting actual growth, and actual rate of growth (AGR) of Flavobacterium psychrophilum. Dampening effect is represented by: a rectangular hyperbola (a), a simple exponential (b) when grown on a TYES liquid medium and a rectangular hyperbola (c), a simple exponential (d) when grown on FLBP liquid medium.

Figure 3

Comparison of actual growth rate (AGR), predicted growth and maximum actual growth rate (s) from liquid media resulting in highest and lowest maximum growth rates (s) from Study 1 and Study 2 when fitting log × hyp and log × exp. Panels (a) and (b) are taken from Study 1, and panels (c) and (d) from Study 2.