Ground state and collective excitations of a dipolar Bose-Einstein condensate in a bubble trap

Abstract

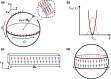
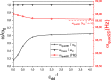
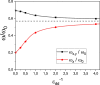
We consider the ground state and the collective excitations of dipolar Bose-Einstein condensates in a bubble trap, i.e., a shell-shaped spherically symmetric confining potential. By means of an appropriate Gaussian ansatz, we determine the ground-state properties in the case where the particles interact by means of both the isotropic and short-range contact and the anisotropic and long-range dipole-dipole potential in the thin-shell limit. Moreover, with the ground state at hand, we employ the sum-rule approach to study the monopole, the two-, the three-dimensional quadrupole as well as the dipole modes. We find situations in which neither the virial nor Kohn's theorem can be applied. On top of that, we demonstrate the existence of anisotropic particle density profiles, which are absent in the case with repulsive contact interaction only. These significant deviations from what one would typically expect are then traced back to both the anisotropic nature of the dipolar interaction and the novel topology introduced by the bubble trap.

Figure 1

(a) Schematic of the bubble trap system under study indicating the coordinate system, polarisation direction of the dipoles, bubble trap (density distribution) mean radius r₀ (R₀) and usual angular coordinates θ and ϕ. Dipoles are spread on the surface of the sphere. For clarity we show dipoles only along a ϕ line along equator and a partial θ line. Inset: detail of the bubble trap with radial cut from which we plot in (b) the harmonic potential landscape (black line) and radial part of the ansatz function Eq. (7) (red dashed line). (c) Schematics of the toy model (see text for detail) showing corresponding coordinate system. (d) Illustration on how the sheet-like toy model “rolls around” the quasi-flat equatorial region of the sphere (see text for details).

Figure 2

(a) Polar distribution of the ground-state particle density |h(θ)|² as a function of the polar angle θ for different values of ϵ_dd. The larger the value of ϵ_dd, the more the particles tend to accumulate along the equator of the sphere. (b) Full width at half maximum of gaussian fits to the ground-state distributions of (a) as a function of ϵ_dd (squares) showing the tendency of the ground state to saturate at a minimum width. Dashed line with open dots are the same quantities obtained by our toy model (see text).

Figure 3

Monopole (downward black triangles) and three-dimensional quadrupole (upward gray triangles) excitation frequencies in units of ω₀ and two-dimensional quadrupole (red circle) in Hz, as functions of ${ϵ}_{\mathrm{dd}}^{-1}$ for ω₀ = 2π × 200 Hz and $\frac{R_0}{R_1}=20$. The curves serve as guides to the eye. For the two-dimensional quadrupole mode, we also indicate the non-dipolar frequency, calculated from the result of ref. , as a horizontal dashed line.

Figure 4

Dipole mode excitation frequencies in units of ω₀ as a function of ${ϵ}_{\mathrm{dd}}^{-1}$.