Theory of relaxor-ferroelectricity

Abstract

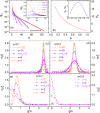
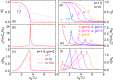
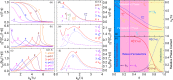
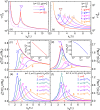
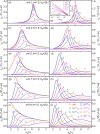
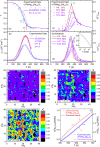
Relaxor-ferroelectrics are fascinating and useful materials, but the mechanism of relaxor-ferroelectricity has been puzzling the scientific community for more than 65 years. Here, a theory of relaxor-ferroelectricity is presented based on 3-dimensional-extended-random-site-Ising-model along with Glauber-dynamics of pseudospins. We propose a new mean-field of pseudospin-strings to solve this kinetic model. The theoretical results show that, with decreasing pseudospin concentration, there are evolutions from normal-ferroelectrics to relaxor-ferroelectrics to paraelectrics, especially indicating by the crossovers from, (a) the sharp to diffuse change at the phase-transition temperature to disappearance in the whole temperature range of order-parameter, and (b) the power-law to Vogel-Fulcher-law to Arrhenius-relation of the average relaxation time. Particularly, the calculated local-order-parameter of the relaxor-ferroelectrics gives the polar-nano-regions appearing far above the diffuse-phase-transition and shows the quasi-fractal characteristic near and below the transition temperature. We also provide a new mechanism of Burns-transformation which stems from not only the polar-nano-regions but also the correlation-function between pseudospins, and put forward a definition of the canonical relaxor-ferroelectrics. The theory accounts for the main facts of relaxor-ferroelectricity, and in addition gives a good quantitative agreement with the experimental results of the order-parameter, specific-heat, high-frequency permittivity, and Burns-transformation of lead magnesium niobate, the canonical relaxor-ferroelectric.

Figure 1

(a) Surface plot of the simulated spatial distributions of PSs (red of height 1) and PS-vacancies (yellow of height 0) in the x-y-plane ($z/a_0=100$) of 3D-RSIM for ϕ $=1/3$ (a 200 × 200 × 200${a_0}^3$ lattice). (b) Simulated PS distribution and connected short PSSs along the x-axis direction in the x-y-plane ($z/a_0=10$) of 3D-RSIM for ϕ $=1/3$ (a small 25 × 25 × 25${a_0}^3$ lattice). Cyan lines and red solid circles show the crystal lattice and PSs, respectively, while the unlabeled lattice points are PS-vacancies. A blue solid square indicates that its nearest-neighbor two PSs belong to the same string; (c) Connected long PSSs in the x-y plane. They are ring PSSs in the circles of (c); and (d) Three PSSs selected from (c). The red circles, blue squares, and violet diamonds show the PSs, the intra-string and inter-string interaction bonds. PSS-1: $n=11$ and $g=11$. PSS-2: $n=24$ and $g=21$. PSS-3: $n=24$ and $g=15$.

Figure 2

(a) q_n vs n in 3D-RSIM with $\varphi =0.1,0.3,05,07,0.9$, and the inset shows $n{q}_n$ vs n for the corresponding ϕ values. $n_p$ is the peak position of $n{q}_n$. (b) $n_0$ vs ϕ in 3D-RSIM, and the inset illustrates E_R vs ϕ. (c–f) $n_n^g$ vs $g/n$ and n in 3D-RSIM with ϕ = 0.1, 0.3, 0.7, and 0.9.

Figure 3

(a) ${\eta }_{ne}^g$, (b) ${\mathit{\chi }}_s^{ng}$, and (c) $c_n^g$ of the n-g-PSSs vs T for $b=1.5$, $g/n=2$, $n=1$ (pink dot line), 10 (blue dash), and 100 (red solid). (d) ${\eta }_{ne}^g$, (e) ${\mathit{\chi }}_s^{ng}$, and (f) $c_n^g$ of the n-g-PSSs vs T for $b=1.5$,$n=10$, $g/n=0$ (red solid line #1), 1 (blue #2), 2 (pink #3), 3 (violet #4), and 4 (orange #5). $T_p^{ng}$ in (a,d) is the DPT temperature.

Figure 4

(a–c) $\eta$, ${\mathit{\chi }}_s^{ps}$, and $c_{ps}$ of 3D-ERSIM with $\varphi =0,0.1,0.3,0.5,0.7,0.9$ vs $T$ for $b=1.5$. (d–f) Order-parameter, static-permittivity, and average specific-heat per PS of 3D-ERSIM, n-0-PSSs, n-1-PSSs, and n-2⁺-PSSs in the model vs $T$ for ϕ = 0.7 and $b=1.5$. $T_p^1$ and $T_p^{2+}$ are the transition temperatures, as well as $T_d^1$ and $T_d^{2+}$ the diffuse temperatures of n-1-PSSs and n-2⁺-PSSs. (g,h) Phase diagram of 3D-ERSIM with $b=1.5$, i.e. $T_p^1$, $T_p^{2+}$, $T_d^1$, $T_d^{2+}$, $R_P^0$, $R_F^1$, $R_F^{2+}$, and $T_b$ vs ϕ. ϕ_e and ϕ_p (PS percolation threshold of 3D-RSIM) are, respectively, the characteristic concentrations of the evolutions between the normal-ferroelectrics $\leftrightarrow$ RFEs $\leftrightarrow$ paraelectrics. ϕ_c (PS-vacancy percolation threshold of 3D-RSIM) is the characteristic concentration of the canonical RFEs (Sec. Inter-PSS interaction distribution and Sec. Definition of canonical RFEs).

Figure 5

(a) Simulated spatial distributions of PSs and PS-vacancies in the x-y-plane ($z/a_0=20$) of 3D-ERSIM for $\varphi =1/3$ and $b=1.5$ (40 × 40 × 40 lattice points). Red and blue squares show the PSs and PS-vacancies, respectively. (b–f) Surface plots of the calculated $s_k^e$ in the x-y-plane when $T=0.5J/k_B=0.14T_p^{2+}$ (b), $3.7J/k_B=T_p^{2+}$ (c), $4.3J/k_B=T_d^{2+}$ (d), $7.4J/k_B=2T_p^{2+}$ (e), and $8.6J/k_B=2T_d^{2+}$ (f).

Figure 6

$\mathrm{\nu }{\tau }_{nn}^g$of n-g-PSSs with $b=1.5$ vs $T$ for $g/n=2$ and $n=2,10,100$ (a), and for $n=10$ and $g/n=0$, 1, 2, 3, 4 (b). (c–f) ${\chi }_n^{g\mathrm{\prime }}$ and ${\mathit{\chi }}_n^{g^{″}}$ of n-g-PSSs with $b=1.5$ and $U_B=20J$ vs T and ω for $n=10$ and $g/n=0$ (c,e), 2 (d,f). $T_m^{ng}$ is the temperature corresponding to the maximum of ${\chi }_n^{g\mathrm{\prime }}$. Insets of (c,d) show $1/T_m^{ng}$ vs ω.

Figure 7

(a,c,e,g,i) ${\mathit{\chi }}_{ps}^{\prime }$ as well as (b,d,f,h,j) ${\mathit{\chi }}_{ps}^{″}$ of 3D-ERSIGM with $b=1.5$, $U_B=20J$, and serial ϕ vs $T$ and serial ω. (a,b) ϕ = 0.1. (c,d) ϕ = 0.3. (e,f) $\varphi =0.5$. (g,h) ϕ $=0.7$. (i,j) ϕ $=0.9$. ω $=0$ (red solid line), ${10}^{-4.0}{\nu }_0$ (blue), ${10}^{-3.5}{\nu }_0$ (deep yellow), ${10}^{-3.0}{\mathrm{\nu }}_0$ (pink), ${10}^{-2.5}{\nu }_0$ (dark green), ${10}^{-2.0}{\mathrm{\nu }}_0$ (orange), and ${10}^{-1.5}{\mathrm{\nu }}_0$ (violet). T_m in (e) is the temperature corresponding to the maximum of ${\mathit{\chi }}_{ps}^{\prime }$. The inset of (b) shows the corresponding $1/T_m$ vs ω.

Figure 8

(a) Red square, blue circle [from Gehring et al. Phys. Rev. B 79, 224109 (2009)], violet diamond, pink star, and cyan asterisk [from Stock et al. Phys. Rev. B 81, 144127 (2010)] points are the experimental data of the order-parameter (η) of PMN single crystals vs temperature (T). The line is the results of 3D-ERSIM with ϕ = 1/3, $J=82\mathrm{K}$, and $b=1.5$. $T_p^{2+}=290\mathrm{K}$ and $T_d^{2+}=341\mathrm{K}$. (b) Red square [from Moriya et al. Phys. Rev. Lett. 90, 205901 (2003)] and blue circle [from Tachibana et al. Phys. Rev. B 80, 094115 (2009)] points are the experimental data of the specific-heat (c_pt) of the DPT of PMN single crystals vs T. The line is the results of 3D-ERSIM with ϕ = 1/3, $J=102\mathrm{K}$, and$b=1.5$. (c) Points are the experimental data of the real part (${\mathit{\chi }}_{exp}^{\prime }$) and (d) imaginary part (${\mathit{\chi }}_{exp}^{″}$) of complex-permittivity of PMN single crystals vs T for frequency (f) = 8, 17, 37, and 74GHz from Bovtun et al. [J. Euro. Cer. Soc. 26, 2867 (2006)]. The lines are the results of 3D-ERSIGM with ϕ = 1/3, $J=87\mathrm{K}$, $b=1.5$, $C_w=3.28\times {10}^3\mathrm{K}$, $U_B=20J$, and ${\nu }_0=2.51\times {10}^{14}\mathrm{H}\mathrm{z}$. The inset of (d) shows the theoretical 1/T_m vs f. (e–g) Surface plots of the calculated $s_k^e$ in a x-y-plane of PMN when $T=620K\approx T_b$, $341K=T_d^{2+}$, and $290K=T_p^{2+}$ according to the 3D-ERSIM for ϕ = 1/3, $J=82\mathrm{K}$ and $b=1.5$. (h) Points are the experimental data of refractive-index ($n_{kl}$, 4880Å) [red squares from H. S. Luo (private communication)] and thermal-strain ($s_{kl}$) [blue circles from L. N. Wang (private communication)] of PMN single crystals vs T. The lines are our theoretical results (Eq. 13a-b), (i) for n_kl: ϕ = 1/3, $J=90\mathrm{K}$, $b=1.5$, $b_{kl}=3.75\times {10}^{-5}$K⁻¹, and$d_{kl}=0.124$, and (ii) for $s_{kl}$: ϕ = 1/3, $J=90\mathrm{K}$, $b=1.5$, ${\alpha }_{kl}=1.32\times {10}^{-5}$K⁻¹, and $c_{kl}=9.81\times {10}^{-3}$.