A hybrid model of intercellular tension and cell-matrix mechanical interactions in a multicellular geometry
- PMID: 32193709
- PMCID: PMC7502553
- DOI: 10.1007/s10237-020-01321-8
A hybrid model of intercellular tension and cell-matrix mechanical interactions in a multicellular geometry
Abstract
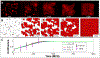
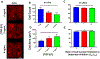
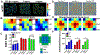
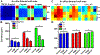
Epithelial cells form continuous sheets of cells that exist in tensional homeostasis. Homeostasis is maintained through cell-to-cell junctions that distribute tension and balance forces between cells and their underlying matrix. Disruption of tensional homeostasis can lead to epithelial-mesenchymal transition (EMT), a transdifferentiation process in which epithelial cells adopt a mesenchymal phenotype, losing cell-cell adhesion and enhancing cellular motility. This process is critical during embryogenesis and wound healing, but is also dysregulated in many disease states. To further understand the role of intercellular tension in spatial patterning of epithelial cell monolayers, we developed a multicellular computational model of cell-cell and cell-substrate forces. This work builds on a hybrid cellular Potts model (CPM)-finite element model to evaluate cell-matrix mechanical feedback of an adherent multicellular cluster. Cellular movement is governed by thermodynamic constraints from cell volume, cell-cell and cell-matrix contacts, and durotaxis, which arises from cell-generated traction forces on a finite element substrate. Junction forces at cell-cell contacts balance these traction forces, thereby producing a mechanically stable epithelial monolayer. Simulations were compared to in vitro experiments using fluorescence-based junction force sensors in clusters of cells undergoing EMT. Results indicate that the multicellular CPM model can reproduce many aspects of EMT, including epithelial monolayer formation dynamics, changes in cell geometry, and spatial patterning of cell-cell forces in an epithelial tissue.
Keywords: Cell mechanics; Cellular Potts model; Cell–cell junction forces; Epithelial–mesenchymal transition; Spatial patterning; Traction forces.
Figures



Similar articles
-
Contact inhibition of locomotion determines cell-cell and cell-substrate forces in tissues.Proc Natl Acad Sci U S A. 2016 Mar 8;113(10):2660-5. doi: 10.1073/pnas.1522330113. Epub 2016 Feb 22. Proc Natl Acad Sci U S A. 2016. PMID: 26903658 Free PMC article.
-
Force localization modes in dynamic epithelial colonies.Mol Biol Cell. 2018 Nov 15;29(23):2835-2847. doi: 10.1091/mbc.E18-05-0336. Epub 2018 Sep 12. Mol Biol Cell. 2018. PMID: 30207837 Free PMC article.
-
Fibronectin fibrils regulate TGF-β1-induced Epithelial-Mesenchymal Transition.Matrix Biol. 2017 Jul;60-61:157-175. doi: 10.1016/j.matbio.2017.01.001. Epub 2017 Jan 19. Matrix Biol. 2017. PMID: 28109697 Free PMC article.
-
LIM-domain proteins in transforming growth factor β-induced epithelial-to-mesenchymal transition and myofibroblast differentiation.Cell Signal. 2012 Apr;24(4):819-25. doi: 10.1016/j.cellsig.2011.12.004. Epub 2011 Dec 11. Cell Signal. 2012. PMID: 22182513 Review.
-
Balancing forces: architectural control of mechanotransduction.Nat Rev Mol Cell Biol. 2011 May;12(5):308-19. doi: 10.1038/nrm3112. Nat Rev Mol Cell Biol. 2011. PMID: 21508987 Free PMC article. Review.
Cited by
-
Immunofluorescence Image Feature Analysis and Phenotype Scoring Pipeline for Distinguishing Epithelial-Mesenchymal Transition.Microsc Microanal. 2021 Aug;27(4):849-859. doi: 10.1017/S1431927621000428. Microsc Microanal. 2021. PMID: 34011419 Free PMC article.
-
A Multicellular Mechanochemical Model to Investigate Tumor Microenvironment Remodeling and Pre-Metastatic Niche Formation.Cell Mol Bioeng. 2024 Nov 13;17(6):573-596. doi: 10.1007/s12195-024-00831-0. eCollection 2024 Dec. Cell Mol Bioeng. 2024. PMID: 39926379
-
Hyperosmotic stress induces epithelial-mesenchymal transition through rearrangements of focal adhesions in tubular epithelial cells.PLoS One. 2021 Dec 21;16(12):e0261345. doi: 10.1371/journal.pone.0261345. eCollection 2021. PLoS One. 2021. PMID: 34932568 Free PMC article.
-
A data-assimilation approach to predict population dynamics during epithelial-mesenchymal transition.Biophys J. 2022 Aug 16;121(16):3061-3080. doi: 10.1016/j.bpj.2022.07.014. Epub 2022 Jul 14. Biophys J. 2022. PMID: 35836379 Free PMC article.
-
Cellular mitosis predicts vessel stability in a mechanochemical model of sprouting angiogenesis.Biomech Model Mechanobiol. 2021 Jun;20(3):1195-1208. doi: 10.1007/s10237-021-01442-8. Epub 2021 Mar 14. Biomech Model Mechanobiol. 2021. PMID: 33715101 Free PMC article.
References
-
- Fristrom D, Tissue and Cell 20(5), 645 (1988). DOI 10.1016/0040-8166(88)90015-8. URL http://www.sciencedirect.com/science/article/pii/0040816688900158 - DOI - PubMed
-
- Ingber DE, Proceedings of the National Academy of Sciences 102(33), 11571 (2005). DOI 10.1073/pnas.0505939102. URL https://www.pnas.org/content/102/33/11571 - DOI - PMC - PubMed
-
- Nelson CM, Jean RP, Tan JL, Liu WF, Sniadecki NJ, Spector AA, Chen CS,Proceedings of the National Academy of Sciences 102(33), 11594 (2005). DOI 10.1073/pnas.0502575102. URL http://www.pnas.org/cgi/doi/10.1073/pnas.0502575102 - DOI - DOI - PMC - PubMed
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources

