Multiple testing correction over contrasts for brain imaging
- PMID: 32201328
- PMCID: PMC8191638
- DOI: 10.1016/j.neuroimage.2020.116760
Multiple testing correction over contrasts for brain imaging
Abstract
The multiple testing problem arises not only when there are many voxels or vertices in an image representation of the brain, but also when multiple contrasts of parameter estimates (that represent hypotheses) are tested in the same general linear model. We argue that a correction for this multiplicity must be performed to avoid excess of false positives. Various methods for correction have been proposed in the literature, but few have been applied to brain imaging. Here we discuss and compare different methods to make such correction in different scenarios, showing that one classical and well known method is invalid, and argue that permutation is the best option to perform such correction due to its exactness and flexibility to handle a variety of common imaging situations.
Keywords: Brain imaging; Contrast correction; Multiple comparisons; Multiple testing; Permutation tests.
Copyright © 2020 The Authors. Published by Elsevier Inc. All rights reserved.
Figures

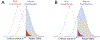
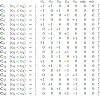






Similar articles
-
Non-parametric combination and related permutation tests for neuroimaging.Hum Brain Mapp. 2016 Apr;37(4):1486-511. doi: 10.1002/hbm.23115. Epub 2016 Feb 5. Hum Brain Mapp. 2016. PMID: 26848101 Free PMC article.
-
Faster permutation inference in brain imaging.Neuroimage. 2016 Nov 1;141:502-516. doi: 10.1016/j.neuroimage.2016.05.068. Epub 2016 Jun 7. Neuroimage. 2016. PMID: 27288322 Free PMC article.
-
False-positive neuroimaging: Undisclosed flexibility in testing spatial hypotheses allows presenting anything as a replicated finding.Neuroimage. 2019 Jul 15;195:384-395. doi: 10.1016/j.neuroimage.2019.03.070. Epub 2019 Apr 2. Neuroimage. 2019. PMID: 30946952
-
Controlling the familywise error rate in functional neuroimaging: a comparative review.Stat Methods Med Res. 2003 Oct;12(5):419-46. doi: 10.1191/0962280203sm341ra. Stat Methods Med Res. 2003. PMID: 14599004 Review.
-
Brain Imaging Quality Assurance: How to Acquire the Best Brain Images Possible.J Nucl Med Technol. 2019 Mar;47(1):13-20. doi: 10.2967/jnmt.118.211771. Epub 2019 Jan 25. J Nucl Med Technol. 2019. PMID: 30683691 Review.
Cited by
-
Medial Prefrontal Cortex Dysfunction Mediates Working Memory Deficits in Patients With Schizophrenia.Biol Psychiatry Glob Open Sci. 2022 Oct 26;3(4):990-1002. doi: 10.1016/j.bpsgos.2022.10.003. eCollection 2023 Oct. Biol Psychiatry Glob Open Sci. 2022. PMID: 37881571 Free PMC article.
-
Multi-spectral diffusion MRI mega-analysis in genetic generalized epilepsy: Relation to outcomes.Neuroimage Clin. 2023;39:103474. doi: 10.1016/j.nicl.2023.103474. Epub 2023 Jul 8. Neuroimage Clin. 2023. PMID: 37441820 Free PMC article.
-
Cerebral Amyloid Angiopathy Is Associated With Higher R2 Relaxation Rate: An MRI and Pathology Study.Ann Clin Transl Neurol. 2025 Jun;12(6):1214-1224. doi: 10.1002/acn3.70037. Epub 2025 Apr 17. Ann Clin Transl Neurol. 2025. PMID: 40244903 Free PMC article.
-
Brainstem white matter microstructure is associated with hyporesponsiveness and overall sensory features in autistic children.Mol Autism. 2022 Dec 19;13(1):48. doi: 10.1186/s13229-022-00524-3. Mol Autism. 2022. PMID: 36536467 Free PMC article.
-
Immediate effect of quadri-pulse stimulation on human brain microstructures and functions.Imaging Neurosci (Camb). 2024 Aug 12;2:imag-2-00264. doi: 10.1162/imag_a_00264. eCollection 2024. Imaging Neurosci (Camb). 2024. PMID: 40800441 Free PMC article.
References
-
- Abdi H, 2007. The bonferonni and Šidák corrections for multiple comparisons. In: Encyclopedia of Measurement and Statistics. SAGE, pp. 1–9.
-
- Barratt W, 2006. The Barratt Simplified Measure of Social Status (BSMSS): Measuring SES. Indiana State University, Unpublished manuscript.
-
- Bonferroni C, 1936. Teoria statistica delle classi e calcolo delle probabilita. Pubblicazioni del R Istituto Superiore di Scienze Economiche e Commericiali di Firenze 8, 3–62.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

