The electronic thickness of graphene

Abstract

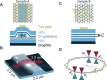
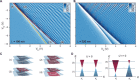
When two dimensional crystals are atomically close, their finite thickness becomes relevant. Using transport measurements, we investigate the electrostatics of two graphene layers, twisted by θ = 22° such that the layers are decoupled by the huge momentum mismatch between the K and K' points of the two layers. We observe a splitting of the zero-density lines of the two layers with increasing interlayer energy difference. This splitting is given by the ratio of single-layer quantum capacitance over interlayer capacitance C _m and is therefore suited to extract C _m. We explain the large observed value of C _m by considering the finite dielectric thickness d _g of each graphene layer and determine d _g ≈ 2.6 Å. In a second experiment, we map out the entire density range with a Fabry-Pérot resonator. We can precisely measure the Fermi wavelength λ in each layer, showing that the layers are decoupled. Our findings are reproduced using tight-binding calculations.

Fig. 1. Experimental design.

(A) Top and side views of two aligned layers of graphene that are decoupled in the middle (blue part) by a thin intermediate layer of hBN. A graphite back gate and a local top gate allow controlling the density and, thereby, the carrier wavelength in the upper and lower layers individually. (B) Using atomic force microscopy (AFM), we measured the encapsulated hBN layer to be 3.5 nm thick (sample A). (C) Alternatively, the decoupling wave functions can be achieved by twisting two graphene layers (sample B). (D) For large twist angles, the valleys in the upper/lower layer (K_t, K_b) are separated by a large momentum, leading to an effective electronic decoupling of the layers.

Fig. 2. Zero-density lines.

Numerical derivative of the two-terminal conductance dG/dV_tg(V_tg, V_bg) for a device where the graphene layers are (A) separated by a thin hBN layer (sample A) or (B) in atomic vicinity but twisted by a large angle (sample B). Zero-density lines in the upper (yellow) and lower (red) graphene layers are obtained from numerical calculations. (C) Schematic electrostatic configuration of sample B. (D) Calculated integrated local density of states ILDOS(z) of p_z-like orbital of carbon atoms in graphene (red) and the induced charge density Δρ(z) ≔ ρ(0) − ρ(E_z) per carbon atom under an external electric field E_z. The geometry of graphene is shown on the background picture. The graphene sheet is placed at z = 0 and extends in the xy plane. Positions of black dotted lines mark the effective thickness of graphene calculated from the expectation value of the position operator $⟨z⟩=0.66 \mathrm{\AA }$. The blue shaded region shows the dielectric thickness of graphene extracted from the dielectric permittivity (19). (E) Comparison of Δρ(z) for bilayer graphene (BLG) in AA stacking configuration (gray line), AB Bernal (blue line), and twisted BLG (tBLG) (red line). The position of graphene layers is marked by vertical dashed lines, and the blue shaded regions depict the dielectric thickness of single-layer graphene. a.u., arbitrary units.

Fig. 3. Fabry-Pérot interference pattern.

Differential conductance dG/dV_tg(V_tg, V_bg) for gates of length (A) L = 190 nm and (B) L = 320 nm for sample B. (C) Sketches of the local density in the two Fabry-Pérot layers. Blue regions are p-doped, and red regions are n-doped. The sketches (1) to (4) show different gating configurations, marked correspondingly in (A). (D) As the difference in gate voltages increases, the energies in the top and bottom layers will shift by the interlayer energy difference U.

Fig. 4. Simulations.

(A) Numerically calculated layer density profiles n_t(x) (blue) and n_b(x) (red), shaped by a top gate with a size of 320 nm and a global back gate for sample A with an hBN spacer (left) and for sample B with a large-angle tBLG (right). The depicted gating condition is (V_tg, V_bg) = (5,5) V. The dashed lines show the classical result (neglecting the quantum capacitance). (B) Interlayer energy difference U(V_tg, V_bg). Zero-density lines are marked with yellow and red lines. (C) Numerical derivative of the calculated normalized conductance, ∂g/∂V_tg. Using the obtained n_t and n_b, the conductance g(V_tg, V_bg) of the top layer (top) and the bottom layer (bottom) are calculated individually using a real-space Green’s function approach. (D) The sum of the two differential conductances ∂g_tot/∂V_tg reproduces the experimental data in Fig. 3B.