No-boarding buses: Synchronisation for efficiency

Abstract

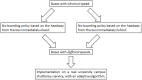
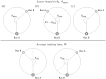
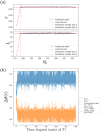
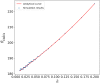
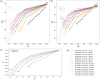
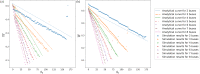
We investigate a no-boarding policy in a system of N buses serving M bus stops in a loop, which is an entrainment mechanism to keep buses synchronised in a reasonably staggered configuration. Buses always allow alighting, but would disallow boarding if certain criteria are met. For an analytically tractable theory, buses move with the same natural speed (applicable to programmable self-driving buses), where the average waiting time experienced by passengers waiting at the bus stop for a bus to arrive can be calculated. The analytical results show that a no-boarding policy can dramatically reduce the average waiting time, as compared to the usual situation without the no-boarding policy. Subsequently, we carry out simulations to verify these theoretical analyses, also extending the simulations to typical human-driven buses with different natural speeds based on real data. Finally, a simple general adaptive algorithm is implemented to dynamically determine when to implement no-boarding in a simulation for a real university shuttle bus service.

Fig 1. Outline and organisation of this paper.

Fig 2. N = 2 buses serving M = 1 bus stop in a loop.

The buses travel clockwise, and implement the no-boarding policy if Δθ > θ₀. Top panel: Shown here is the situation where θ₀ is the lower bound θ_min, before the system is picking up people slower than people arriving at the bus stops. Bottom panel: In steady state, the phase difference Δθ(t) fluctuates around the effective angle θ_eff, which is bounded by θ₀ (i.e. θ_eff < θ₀). On average, bus A and bus B would stop over the same duration τ and pick up the same number of people L. Since bus B is lagging due to its large phase difference with respect to bus A, a portion of (1 − π/θ_eff) × 100% of the people waiting for bus B would have to wait longer to board bus A instead, because bus B would have implemented the no-boarding policy when Δθ > θ₀. Hence if θ_eff is closer to π, then fewer people would have to be denied boarding by bus B. A closer-to-antipodal configuration would improve the overall average waiting time, given by Eq (15).

Fig 3

(a) Graphs of $\overline{\tau }$ and L versus θ₀ for each of the two buses. These simulation results agree with Eqs (4) and (5), as well as the lower bound θ_min from Eq (7). Shown here [as well as in (b)] is for k = 1/16, and these features similarly hold for any value of (fixed) k. (b) Graphs of Δθ(t) versus time for each of the two buses. The no-boarding policy kicks in if Δθ > 225°.

Fig 4. Graphs of W¯ versus: (a) θ₀, (c) the mean, as well as (d) median phase differences, respectively.

The effective phase difference θ_eff during steady state being the median phase difference between the two buses more closely matches the predicted value from Eq (15), compared to the mean phase difference. Note that below the lower bound θ₀ = θ_min, $\overline{W}$ blows up by two orders of magnitude (not plotted): $\overline{W}=10.4$ at θ₀ = 191°, $\overline{W}=31.5$ at θ₀ = 190°, $\overline{W}=54.6$ at θ₀ = 189°, …. Similar graphs can be obtained for any value of k. (b) The relationship between θ₀ and the mean as well as median phase differences as measured from the simulations.

Fig 5. Graph of θ_min versus k.

Fig 6

(a) Simulation results for N = 2, 3, 4, 5, 6, 7, 8 buses, respectively, serving M = 1 bus stop. The demand level is fixed at k = 1/16. (b) Simulation results for N = 2, 3, 4, 5, 6, 7, 8 buses, respectively, serving M = 12 bus stops. The demand level is fixed at k = 1/100. The analytical curves are for those serving M = 1 bus stop. The simulation points have average waiting times which are higher than their corresponding analytical curves, since these buses serve M = 12 bus stops. Furthermore, there are discrete jumps on the simulation points whenever an extra bus stop is present. (c) Graphs of the piecewise continuous curves for N = 2, 3, 4, 5 as given by Eq (18) with $\overline{\tau }/4$ subtracted away, together with the corresponding smooth curves Eq (18) that pass through the boundary points of each line segment, for the respective N. These smooth curves are hyperbolas, and approach an “L”-shaped asymptotic curve as N → ∞. (d) Legend for (a) and (b).

Fig 7

(a) Simulation results for N = 2, 3, 4, 5, 6, 7, 8 buses, respectively, serving M = 1 bus stop. The demand level is fixed at k = 1/16. (b) Simulation results for N = 2, 3, 4, 5, 6, 7, 8 buses, respectively, serving M = 12 bus stops. The demand level is fixed at k = 1/100. The analytical curves are those serving M = 1 bus stop. The simulation points have average waiting times which are higher than their corresponding analytical curves, since these buses serve M = 12 bus stops. Furthermore, there are discrete jumps on the simulation points whenever an extra bus stop is present.

Fig 8

(a) Simulation results for N = 2, 3, 6 buses, respectively, serving M = 12 bus stops in a loop. The no-boarding policy is applied by looking at the bus immediately ahead. Note that θ₀ = 360° corresponds to no-implementation. The left column is in the lull phase where the no-boarding policy backfires and increases the passenger waiting time, as compared to no implentation (or 360°). On the other hand, the right column is in the busy phase where the no-boarding policy correctly reduces the average waiting time as expected, by preventing the buses from forming permanent bunched clusters. (b) The corresponding simulation results as in (a), but with the no-boarding policy by looking at the bus immediately behind. Note that θ₀ = 0° corresponds to no-implementation.

Fig 9

Top row: Graphs of best and actual expected θ₀ versus time for lull (left), busy (middle), and a lull case with frequency detuning (right). Bottom: Graphs of best and actual expected average waiting time versus time for lull (left), busy (middle), and a lull case with frequency detuning (right). In each plot, the actual curve is the thin dotted curve, whereas the best expected curve is the thick curve. The red horizontal line in the bottom graphs represents the average waiting time when the no-boarding policy is not implemented.