Generalization error analysis for deep convolutional neural network with transfer learning in breast cancer diagnosis
- PMID: 32208369
- PMCID: PMC7981191
- DOI: 10.1088/1361-6560/ab82e8
Generalization error analysis for deep convolutional neural network with transfer learning in breast cancer diagnosis
Abstract
Deep convolutional neural network (DCNN), now popularly called artificial intelligence (AI), has shown the potential to improve over previous computer-assisted tools in medical imaging developed in the past decades. A DCNN has millions of free parameters that need to be trained, but the training sample set is limited in size for most medical imaging tasks so that transfer learning is typically used. Automatic data mining may be an efficient way to enlarge the collected data set but the data can be noisy such as incorrect labels or even a wrong type of image. In this work we studied the generalization error of DCNN with transfer learning in medical imaging for the task of classifying malignant and benign masses on mammograms. With a finite available data set, we simulated a training set containing corrupted data or noisy labels. The balance between learning and memorization of the DCNN was manipulated by varying the proportion of corrupted data in the training set. The generalization error of DCNN was analyzed by the area under the receiver operating characteristic curve for the training and test sets and the weight changes after transfer learning. The study demonstrates that the transfer learning strategy of DCNN for such tasks needs to be designed properly, taking into consideration the constraints of the available training set having limited size and quality for the classification task at hand, to minimize memorization and improve generalizability.
Figures





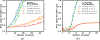
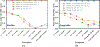

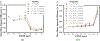

Similar articles
-
Mass detection in digital breast tomosynthesis: Deep convolutional neural network with transfer learning from mammography.Med Phys. 2016 Dec;43(12):6654. doi: 10.1118/1.4967345. Med Phys. 2016. PMID: 27908154 Free PMC article.
-
Digital breast tomosynthesis versus digital mammography: integration of image modalities enhances deep learning-based breast mass classification.Eur Radiol. 2020 Feb;30(2):778-788. doi: 10.1007/s00330-019-06457-5. Epub 2019 Nov 5. Eur Radiol. 2020. PMID: 31691121
-
Multi-task transfer learning deep convolutional neural network: application to computer-aided diagnosis of breast cancer on mammograms.Phys Med Biol. 2017 Nov 10;62(23):8894-8908. doi: 10.1088/1361-6560/aa93d4. Phys Med Biol. 2017. PMID: 29035873 Free PMC article.
-
Convolutional neural networks for computer-aided detection or diagnosis in medical image analysis: An overview.Math Biosci Eng. 2019 Jul 15;16(6):6536-6561. doi: 10.3934/mbe.2019326. Math Biosci Eng. 2019. PMID: 31698575 Review.
-
Deep Learning Computer-Aided Diagnosis for Breast Lesion in Digital Mammogram.Adv Exp Med Biol. 2020;1213:59-72. doi: 10.1007/978-3-030-33128-3_4. Adv Exp Med Biol. 2020. PMID: 32030663 Review.
Cited by
-
Breast lesions classifications of mammographic images using a deep convolutional neural network-based approach.PLoS One. 2022 Jan 27;17(1):e0263126. doi: 10.1371/journal.pone.0263126. eCollection 2022. PLoS One. 2022. PMID: 35085352 Free PMC article.
-
Homogenization of multi-institutional chest x-ray images in various data transformation schemes.J Med Imaging (Bellingham). 2023 Nov;10(6):061103. doi: 10.1117/1.JMI.10.6.061103. Epub 2023 Apr 26. J Med Imaging (Bellingham). 2023. PMID: 37125408 Free PMC article.
-
Vision-Transformer-Based Transfer Learning for Mammogram Classification.Diagnostics (Basel). 2023 Jan 4;13(2):178. doi: 10.3390/diagnostics13020178. Diagnostics (Basel). 2023. PMID: 36672988 Free PMC article.
-
Machine learning and new insights for breast cancer diagnosis.J Int Med Res. 2024 Apr;52(4):3000605241237867. doi: 10.1177/03000605241237867. J Int Med Res. 2024. PMID: 38663911 Free PMC article. Review.
-
Deep learning with noisy labels in medical prediction problems: a scoping review.J Am Med Inform Assoc. 2024 Jun 20;31(7):1596-1607. doi: 10.1093/jamia/ocae108. J Am Med Inform Assoc. 2024. PMID: 38814164 Free PMC article.
References
-
- Byra M, Styczynski G, Szmigielski C, Kalinowski P, Michałowski Ł, Paluszkiewicz R, Ziarkiewicz-Wróblewska B, Zieniewicz K, Sobieraj P and Nowicki A 2018. Transfer learning with deep convolutional neural network for liver steatosis assessment in ultrasound images Int J Comput Ass Rad 13 1895–903 - PMC - PubMed
-
- Chan H-P, Lo S C, Helvie M, Goodsitt M M, Cheng S N C and Adler D D 1993. Recognition of mammographic microcalcifications with artificial neural network Radiology 189(P) 318
-
- Chan H-P, Lo S C B, Sahiner B, Lam K L and Helvie M A 1995a. Computer-aided detection of mammographic microcalcifications: Pattern recognition with an artificial neural network Medical Physics 22 1555–67 - PubMed
-
- Chan H-P, Sahiner B, Lo S C, Helvie M, Petrick N, Adler D D and Goodsitt M M 1994. Computer-aided diagnosis in mammography: detection of masses by artificial neural network Medical Physics 21 875–6
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Medical
Miscellaneous
