Scale-invariant topology and bursty branching of evolutionary trees emerge from niche construction
- PMID: 32209672
- PMCID: PMC7149460
- DOI: 10.1073/pnas.1915088117
Scale-invariant topology and bursty branching of evolutionary trees emerge from niche construction
Abstract
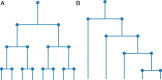
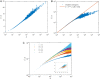
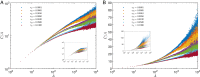
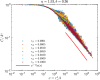
Phylogenetic trees describe both the evolutionary process and community diversity. Recent work has established that they exhibit scale-invariant topology, which quantifies the fact that their branching lies in between the two extreme cases of balanced binary trees and maximally unbalanced ones. In addition, the backbones of phylogenetic trees exhibit bursts of diversification on all timescales. Here, we present a simple, coarse-grained statistical model of niche construction coupled to speciation. Finite-size scaling analysis of the dynamics shows that the resultant phylogenetic tree topology is scale-invariant due to a singularity arising from large niche construction fluctuations that follow extinction events. The same model recapitulates the bursty pattern of diversification in time. These results show how dynamical scaling laws of phylogenetic trees on long timescales can reflect the indelible imprint of the interplay between ecological and evolutionary processes.
Keywords: evolution; molecular phylogeny; niche construction; scaling laws.
Figures
Similar articles
-
How Ecology and Landscape Dynamics Shape Phylogenetic Trees.Syst Biol. 2015 Jul;64(4):590-607. doi: 10.1093/sysbio/syv014. Epub 2015 Mar 13. Syst Biol. 2015. PMID: 25771083
-
The shape and temporal dynamics of phylogenetic trees arising from geographic speciation.Syst Biol. 2010 Dec;59(6):660-73. doi: 10.1093/sysbio/syq058. Epub 2010 Oct 15. Syst Biol. 2010. PMID: 20952757
-
What defines an adaptive radiation? Macroevolutionary diversification dynamics of an exceptionally species-rich continental lizard radiation.BMC Evol Biol. 2015 Aug 7;15:153. doi: 10.1186/s12862-015-0435-9. BMC Evol Biol. 2015. PMID: 26245280 Free PMC article.
-
Phylogenetic estimates of speciation and extinction rates for testing ecological and evolutionary hypotheses.Trends Ecol Evol. 2013 Dec;28(12):729-36. doi: 10.1016/j.tree.2013.09.007. Epub 2013 Oct 10. Trends Ecol Evol. 2013. PMID: 24120478 Review.
-
How traits shape trees: new approaches for detecting character state-dependent lineage diversification.J Evol Biol. 2014 Oct;27(10):2035-45. doi: 10.1111/jeb.12460. Epub 2014 Jul 25. J Evol Biol. 2014. PMID: 25066512 Review.
Cited by
-
Human pathogenic RNA viruses establish noncompeting lineages by occupying independent niches.Proc Natl Acad Sci U S A. 2022 Jun 7;119(23):e2121335119. doi: 10.1073/pnas.2121335119. Epub 2022 May 31. Proc Natl Acad Sci U S A. 2022. PMID: 35639694 Free PMC article.
-
Environmental fluctuations explain the universal decay of species-abundance correlations with phylogenetic distance.Proc Natl Acad Sci U S A. 2023 Sep 12;120(37):e2217144120. doi: 10.1073/pnas.2217144120. Epub 2023 Sep 5. Proc Natl Acad Sci U S A. 2023. PMID: 37669363 Free PMC article.
References
-
- Haig D., Hurst L. D., A quantitative measure of error minimization in the genetic code. J. Mol. Evol. 33, 412–417 (1991). - PubMed
-
- Koonin E. V., Novozhilov A. S., Origin and evolution of the universal genetic code. Annu. Rev. Genet. 51, 45–62 (2017). - PubMed
-
- Hernandez-Garcia E., Tuğrul M., Alejandro Herrada E., Eguiluz V. M., Klemm K., Simple models for scaling in phylogenetic trees. Int. J. Bifurcation Chaos 20, 805–811 (2010).
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources

