Foraging optimally in social neuroscience: computations and methodological considerations

Abstract

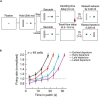
Research in social neuroscience has increasingly begun to use the tools of computational neuroscience to better understand behaviour. Such approaches have proven fruitful for probing underlying neural mechanisms. However, little attention has been paid to how the structure of experimental tasks relates to real-world decisions, and the problems that brains have evolved to solve. To go significantly beyond current understanding, we must begin to use paradigms and mathematical models from behavioural ecology, which offer insights into the decisions animals must make successfully in order to survive. One highly influential theory-marginal value theorem (MVT)-precisely characterises and provides an optimal solution to a vital foraging decision that most species must make: the patch-leaving problem. Animals must decide when to leave collecting rewards in a current patch (location) and travel somewhere else. We propose that many questions posed in social neuroscience can be approached as patch-leaving problems. A richer understanding of the neural mechanisms underlying social behaviour will be obtained by using MVT. In this 'tools of the trade' article, we outline the patch-leaving problem, the computations of MVT and discuss the application to social neuroscience. Furthermore, we consider the practical challenges and offer solutions for designing paradigms probing patch leaving, both behaviourally and when using neuroimaging techniques.

Keywords: computational neuroscience; marginal value theorem; optimal foraging theory; social neuroscience.

Box 1: Marginal Value Theorem

Fig. 1

Example patch-leaving paradigms. Left panel – a continuous reward depletion design. Taken from Le Heron et al. (2019), (A) participants had to decide how long to remain in their current patch (field). Reward (milk) gains were indicated by the continuous filling of the silver bucket with a white bar. This gain occurred at an exponentially decreasing rate. Following a leave decision, a clock ticking down the 6-s travel time was presented, during which they could collect no reward. (B) Three foreground patch types were used, differing in the initial reward rate (low, medium and high yield). Two different background environments (farms) were used, with the background reward rate determined by the relative proportions of these patch types. Percentages represent the distribution of patch types in each environment. (C) Predictions of the optimal leaving times according to MVT. Participants should leave each patch when the instantaneous reward rate in that patch (grey lines) drops to the background environmental average (gold and green dotted lines). Therefore, people should leave sooner from all patches in rich (gold dotted line) compared to poor (green dotted line) environments, but later in high-yield compared to low-yield patches (D) In line with MVT, residency times are longer in higher yield patches, but lower in the rich environment. Right panel. Taken from Constantino and Daw (2015). (E) Participants foraged for apples in virtual patch-foraging environments. On each trial, they could choose to harvest a tree or move on to a new tree. Harvesting returned an exponentially diminishing number of apples with a short time cost. Moving to a different tree incurred a longer time cost. (F) Number of apples at last harvest is indicative of time spent in harvesting. The lower the number, the longer participants spent in harvesting each tree in that environment. Participants foraged each patch longer in richer environments (short travel times, slow decay rates)

Fig. 2

From Hayden et al. (2011). (A) Macaques performed a simulated patch-leaving task. On each trial, the animal could choose to stay or leave a patch by shifting their gaze to either the blue square (stay) or grey rectangle (leave). If they chose to stay, they received juice reward after a short delay, which diminished with each stay decision. If they chose to leave, they incurred a travel cost to the next patch. (B) Average firing rate of population of neurons in area 24 of the anterior cingulate sulcus. Trials split by earliness of patch leaving. Firing rates rose faster for those trials where leave decisions were made earlier, but asymptote at the same level. Error bars represent SEM.

Fig. 3

From Wittmann et al. (2016). (A) Trial structure: participants saw a series of ‘reward events’. These gave rewards of different levels, including no reward. Participants could infer the reward rate by the interval between rewarded events and the magnitude of the rewards. After a fixed period, they chose between staying in the current patch or moving to a previously learned default patch. (B) Trials were derived from 18 different reward curves, nine of which increased, nine of which decreased, monotonically. This approach allowed for decorrelation between the foreground reward rates in different patches. The decision time is indicated by the solid black line, and the default reward rate is indicated by the dotted black line. (C) The dACC showed greater activity with a greater positive reward trend.