Multiview learning for understanding functional multiomics

Abstract

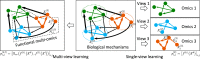
The molecular mechanisms and functions in complex biological systems currently remain elusive. Recent high-throughput techniques, such as next-generation sequencing, have generated a wide variety of multiomics datasets that enable the identification of biological functions and mechanisms via multiple facets. However, integrating these large-scale multiomics data and discovering functional insights are, nevertheless, challenging tasks. To address these challenges, machine learning has been broadly applied to analyze multiomics. This review introduces multiview learning-an emerging machine learning field-and envisions its potentially powerful applications to multiomics. In particular, multiview learning is more effective than previous integrative methods for learning data's heterogeneity and revealing cross-talk patterns. Although it has been applied to various contexts, such as computer vision and speech recognition, multiview learning has not yet been widely applied to biological data-specifically, multiomics data. Therefore, this paper firstly reviews recent multiview learning methods and unifies them in a framework called multiview empirical risk minimization (MV-ERM). We further discuss the potential applications of each method to multiomics, including genomics, transcriptomics, and epigenomics, in an aim to discover the functional and mechanistic interpretations across omics. Secondly, we explore possible applications to different biological systems, including human diseases (e.g., brain disorders and cancers), plants, and single-cell analysis, and discuss both the benefits and caveats of using multiview learning to discover the molecular mechanisms and functions of these systems.

Fig 1. Multiview learning deciphers mechanisms across functional omics.

Molecular mechanisms (Center) are resulted from the interactions within and across multiomics, e.g., shown by green, orange, and blue color. The interactions within each omics are illustrated by colored links that matches with the color of that omics; the interactions across different omics are demonstrated by black links. Directed edges represent causal relationships. Edge weights represent relationship strengths. The single-view learning methods (Right) can only learn the within-view interactions separately for each omics via the functions f^(k),k = 1,2,3 (e.g., $p_{i,j}^{\left(3\right)}={\left[f^{\left(3\right)}\left({\mathcal{X}}^{\left(3\right)}\right)\right]}_{i,j}$). The multiview learning methods (Left) can reveal the cross-talk patterns among various omics, providing complete mechanistic insights on biological functions, e.g., by co-regularization terms Ω_co. These cross-talk patterns are contributed by each facet of learning in either alignment-based methods or factorization-based methods. For example, gene regulatory mechanism can relate to genomics (e.g., regulatory variants), transcriptomics (e.g., gene expression), and proteomics (e.g., TFs). Then Ω_co(f⁽²⁾,f⁽³⁾) represents that variants (e.g., SNPs) break the TFBSs (e.g., $p_{i,j}^{\left(\mathrm{2,3}\right)}={\left[{\Omega }_{co}\left(f^{\left(2\right)}\left({\mathcal{X}}^{\left(2\right)}\right),f^{\left(3\right)}\left({\mathcal{X}}^{\left(3\right)}\right)\right)\right]}_{i,j}$ as in the figure). Ω_co(f⁽¹⁾,f⁽³⁾) represents that variants affect gene expression (e.g., eQTLs). Ω_co(f⁽¹⁾,f⁽²⁾) represents that TFs control target gene expression. The multiview learning can thus predict gene regulatory mechanisms across omics on how variants break TFBSs to affect gene expression. eQTL, expression quantitative trait loci; SNP, single-nucleotide polymorphism; TF, transcription factor; TFB, transcription factor binding site.

Fig 2. MV-ERM.

(A) ERM for single-view learning. It demonstrates a general single-view learning algorithm (based on ERM estimator) that takes one data set ${\mathcal{X}}^{\left(1\right)}$ as input, adopts a hypothesis space ${\mathcal{F}}^{\left(1\right)}$ and a loss function $\mathcal{l}$, and outputs a function $f^{\left(1\right)}\in {\mathcal{F}}^{\left(1\right)}$ that predicts the label associated with any new datapoint x as f⁽¹⁾(x). (B) MV-ERM demonstrates a general multiview learning algorithm (based on MV-ERM estimator) that takes v datasets ${\mathcal{X}}^{\left(1\right)},\dots ,{\mathcal{X}}^{\left(v\right)}$ as v views, adopts v hypothesis spaces ${\mathcal{F}}^{\left(1\right)},\dots ,{\mathcal{F}}^{\left(v\right)}$ associated with v views, and outputs v functions $\left(f^{\left(1\right)},\dots ,f^{\left(v\right)}\right)\in {\mathcal{F}}^{\left(1\right)}\times \dots \times {\mathcal{F}}^{\left(v\right)}$ that reveals the interactions within and between each pair of datasets (via the terms Ω_co(f⁽ⁱ⁾,f^(j)). The consensus and complementary principles are implemented by the term Ω(f⁽ⁱ⁾) and Ω_co(f⁽ⁱ⁾,f^(j)) respectively. Note that in MV-ERM estimator, the loss function is optional because multiview learning can be unsupervised. ERM, empirical risk minimization; MV-ERM, multiview empirical risk minimization.

Fig 3. Factorization-based versus alignment-based methods.

(A) Factorization-based single-view learning methods. They typically factorize a data matrix X from single view (e.g., gene expression matrix of samples by genes) into a product of matrix G (coefficient matrix) and matrix $\tilde{F}$ (dictionary matrix or pattern matrix). Because matrix factorization has an intrinsic clustering property [8], the matrix $\tilde{F}$ can represent a clustering structure of the view (i.e., the soft clustering assignments or indicators). For example, $\tilde{F}$ reveals 3 different gene clusters, a, b, and c, as denoted in the figure. (B) Factorization-based multiview learning methods. They factorize different matrices from multiomics, e.g., gene expression X⁽¹⁾ (i.e., green matrix), protein expression X⁽²⁾ (i.e., blue matrix), and chromatin accessibility X⁽³⁾ (i.e., orange matrix), into a product of different coefficient matrices G^(k)(k = 1,2,3) and the common dictionary matrix $\tilde{F}$. This common representation enables revealing of cross-talk patterns among genes, proteins (more precisely, TFs), and regulatory elements (i.e., enhancers); e.g., a TF binds to a region to regulate a gene's expression. (C) Alignment-based multiview learning methods. The 3 input omic matrices are projected via functions f^(k)(k = 1,2,3) onto spaces where their internal relationships are revealed. These representations of different omics are pairwise coordinated to each other via the term Ω_co. For example, the figure demonstrates the pairwise alignments between X⁽¹⁾, X⁽²⁾ and between X⁽²⁾, X⁽³⁾ to reveal cross-talk patterns between TFs and enhancers, and between enhancers and gene expressions. (Alignment between X⁽¹⁾ and X⁽³⁾ is not shown for making the figure concise.) TF, transcription factor.