Scaling diffraction data in the DIALS software package: algorithms and new approaches for multi-crystal scaling
- PMID: 32254063
- PMCID: PMC7137103
- DOI: 10.1107/S2059798320003198
Scaling diffraction data in the DIALS software package: algorithms and new approaches for multi-crystal scaling
Abstract
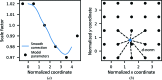
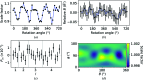
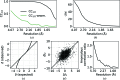
In processing X-ray diffraction data, the intensities obtained from integration of the diffraction images must be corrected for experimental effects in order to place all intensities on a common scale both within and between data collections. Scaling corrects for effects such as changes in sample illumination, absorption and, to some extent, global radiation damage that cause the measured intensities of symmetry-equivalent observations to differ throughout a data set. This necessarily requires a prior evaluation of the point-group symmetry of the crystal. This paper describes and evaluates the scaling algorithms implemented within the DIALS data-processing package and demonstrates the effectiveness and key features of the implementation on example macromolecular crystallographic rotation data. In particular, the scaling algorithms enable new workflows for the scaling of multi-crystal or multi-sweep data sets, providing the analysis required to support current trends towards collecting data from ever-smaller samples. In addition, the implementation of a free-set validation method is discussed, which allows the quantification of the suitability of scaling-model and algorithm choices.
Keywords: crystallography; data analysis; diffraction; multi-crystal; scaling.
open access.
Figures


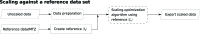

References
-
- Blessing, R. H. (1995). Acta Cryst. A51, 33–38. - PubMed
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources

