Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2019 Dec:32:4869-4880.

Hyperbolic Graph Convolutional Neural Networks

Ines Chami  1 , Rex Ying  2 , Christopher Ré  2 , Jure Leskovec  2
Affiliations

Hyperbolic Graph Convolutional Neural Networks

Ines Chami et al. Adv Neural Inf Process Syst. 2019 Dec.

Abstract

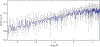
Graph convolutional neural networks (GCNs) embed nodes in a graph into Euclidean space, which has been shown to incur a large distortion when embedding real-world graphs with scale-free or hierarchical structure. Hyperbolic geometry offers an exciting alternative, as it enables embeddings with much smaller distortion. However, extending GCNs to hyperbolic geometry presents several unique challenges because it is not clear how to define neural network operations, such as feature transformation and aggregation, in hyperbolic space. Furthermore, since input features are often Euclidean, it is unclear how to transform the features into hyperbolic embeddings with the right amount of curvature. Here we propose Hyperbolic Graph Convolutional Neural Network (HGCN), the first inductive hyperbolic GCN that leverages both the expressiveness of GCNs and hyperbolic geometry to learn inductive node representations for hierarchical and scale-free graphs. We derive GCNs operations in the hyperboloid model of hyperbolic space and map Euclidean input features to embeddings in hyperbolic spaces with different trainable curvature at each layer. Experiments demonstrate that HGCN learns embeddings that preserve hierarchical structure, and leads to improved performance when compared to Euclidean analogs, even with very low dimensional embeddings: compared to state-of-the-art GCNs, HGCN achieves an error reduction of up to 63.1% in ROC AUC for link prediction and of up to 47.5% in F1 score for node classification, also improving state-of-the art on the Pubmed dataset.

PubMed Disclaimer

Figures

Figure 1:
Figure 1:
Left: Poincaré disk geodesics (shortest path) connecting x and y for different curvatures. As curvature (−1/K) decreases, the distance between x and y increases, and the geodesics lines get closer to the origin. Center: Hyperbolic distance vs curvature. Right: Poincaré geodesic lines. x
Figure 2:
Figure 2:
HGCN neighborhood aggregation (Eq. 9) first maps messages/embeddings to the tangent space, performs the aggregation in the tangent space, and then maps back to the hyperbolic space.
Figure 3:
Figure 3:
Visualization of embeddings for LP on DISEASE and NC on CORA (visualization on the Poincaré disk for HGCN). (a) GCN embeddings in first and last layers for DISEASE LP hardly capture hierarchy (depth indicated by color). (b) In contrast, HGCN preserves node hierarchies. (c) On CORA NC, HGCN leads to better class separation (indicated by different colors).
Figure 4:
Figure 4:
Decreasing curvature (−1/K) improves link prediction performance on DISEASE.
Figure 5:
Figure 5:
Attention: Euclidean GAT (left), HGCN (right). Each graph represents a 2-hop neighborhood of the DISEASE-M dataset.
Figure 6:
Figure 6:
From left to right: a surface of negative curvature, a surface of zero curvature, and a surface of positive curvature.
Figure 7:
Figure 7:
Illustration of the hyperboloid model (top) in 3 dimensions and its connection to the Poincaré disk (bottom).
See this image and copyright information in PMC

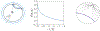
References

    1. Adcock Aaron B, Sullivan Blair D, and Mahoney Michael W. Tree-like structure in large social and information networks. In 2013 IEEE 13th International Conference on Data Mining, pages 1–10. IEEE, 2013.
    1. Anderson Roy M and May Robert M. Infectious diseases of humans: dynamics and control. Oxford university press, 1992.
    1. Belkin Mikhail and Niyogi Partha. Laplacian eigenmaps and spectral techniques for embedding and clustering. In Advances in neural information processing systems, pages 585–591, 2002.
    1. Bonnabel Silvere. Stochastic gradient descent on riemannian manifolds. IEEE Transactions on Automatic Control, 2013.
    1. Benjamin Paul Chamberlain James Clough, and Deisenroth Marc Peter. Neural embeddings of graphs in hyperbolic space. arXiv preprint arXiv:1705.10359, 2017.

LinkOut - more resources