Tunable Thermal Transport Characteristics of Nanocomposites

Abstract

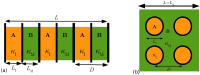
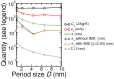
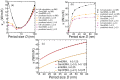
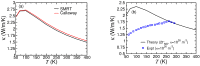
We present a study of tunable thermal transport characteristics of nanocomposites by employing a combination of a full-scale semi-ab inito approach and a generalised and extended modification of the effective medium theory. Investigations are made for planar superlattices (PSLs) and nanodot superlattices (NDSLs) constructed from isotropic conductivity covalent materials Si and Ge, and NDSLs constructed from anisotropic conductivity covalent-van der Waals materials MoS 2 and WS 2 . It is found that difference in the conductivities of individual materials, period size, volume fraction of insertion, and atomic-level interface quality are the four main parameters to control phonon transport in nanocomposite structures. It is argued that the relative importance of these parameters is system dependent. The equal-layer thickness Si/Ge PSL shows a minimum in the room temperature conductivity for the period size of around 4 nm, and with a moderate amount of interface mass smudging this value lies below the conductivity of SiGe alloy.

Keywords: Boltzmann equation; DFT; effective medium theory; nanocomposites; phonons; thermal transport.

Figure 1

Schematic illustration of: (a) a A/B planar superlattice (PSL) structure and (b) a nanodot superlattice (NDSL) structure. L represents sample length and D represents size of a unit cell. We consider A as insert of size $L_I$ and conductivity ${\kappa }_I$, and B as matrix of size $L_M$ and conductivity ${\kappa }_M$.

Figure 2

Schematic illustration of relative sizes of repeat period D and phonon mean free path (MFP) $\Lambda$ for a A/B planar superlattice: (a) $D>>\Lambda$, (b) $D\sim \Lambda$, and (c) $D<<\Lambda$.

Figure 3

Atomic structure of the Si(D/2)/Ge(D/2)[001] planar superlatiice, with unit cell size $D=4.4$ nm containing 8 bilayers of Si and 8 bilayers of Ge. Mass smudging has been considered between only the fist interface atomic layers, i.e., in the regions encircled in red.

Figure 4

Period size dependence of cross-plane room-temperature thermal conductivity for: (a) Si(D/2)Ge(D/2) PSL; (b) NDSL (Ge insert of volume fraction $f=0.125$ in Si matrix); and (c) TMD NDSL ($f=0.125$ of WS${}_2$ inserted in MoS${}_2$). Sample size L is 1 mm the Si/Ge composites in (a,b), and 100 mm for the MoS${}_2$/WS${}_2$ composite in (c). Regions R1, R2 and R3 correspond to $D<<\Lambda$, $D\sim \Lambda$ and $D>>\Lambda$, respectively, where D is repeat period and $\Lambda$ represents phonon mean free path. Results in panel (a) for the Si/Ge PSL are obtained from full-scale DFT-Boltzmann calculation in Region R1, and from the EMA method in Regions R2 and R3. Results in panels (b,c) are obtained from the EMA method.

Figure 5

Variation with period size D, for Si($D/2$)Ge($D/2$) PSL at room temperature, of phonon specific heat ($C_v$), cross-plane velocity component ($|c_z|$), occupation weighted mean free path ($\Lambda$), occupation weighted cross-plane mean free path (${\Lambda }_z$) with sharp interfaces, cross-plane mean free path (${\Lambda }_z$) with 10% atomic mixing across interface ($\zeta =2.3$), and interface density $\Sigma$. Sample size is $L=1$ mm.

Figure 6

Panels (a,b): Comparison of period size dependence of room-temperature cross-plane conductivity for Si($D/2$)/Ge($D/2$) PSL using the EMA, mEMA and emEMA methods. Panel (c): Period and volume fraction dependence of $\kappa$ for Ge ND inserts in Si matrix. Sample size is 1 mm for panel (a) and 500 nm for panels (b,c).

Figure 7

Period size dependence of room-temperature ${\kappa }_{\mathrm{zz}}$ for sample size 500 nm: (a) for Si($D/2$)/Ge($D/2$) PSL, with various amounts of interface mass smudging (IMS); (b) Ge/Si NDSL, with Ge insert fraction of f = 0.125; (c) MoS${}_2$/WS${}_2$ NDSL, with WS${}_2$ insert fraction of f = 0.125. Boundary and interface scattering rates are calculated with the choice of the inhomogeneity factor $\eta =2$. In panel (b) the shape of the smallest Ge insert was cubic.

Figure 8

Thermal conductivity of Si(2.2 nm)/Ge(2.2 nm) PSL, with smaple size $L=400$ nm, n-type doping concentration $n={10}^{26}$ m${}^{-3}$, and IMS factor $\zeta =2.3$. (a) Results are presented using both SMRT and Callaway theories with $L=400$ nm. (b) Comparison between Callaway theory (this study) and experiment (Ref. [33]), with point mass defect concentration taken as twice of the isotopic mass factor and $L=300$ nm.