Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2020 Apr 3;13(7):1674.
doi: 10.3390/ma13071674.

Microstructure Simulation and Constitutive Modelling of Magnetorheological Fluids Based on the Hexagonal Close-packed Structure

Jintao Zhang  1 , Wanli Song  1 , Zhen Peng  1 , Jinwei Gao  1 , Na Wang  1 , Seung-Bok Choi  2 , Gi-Woo Kim  2
Affiliations

Microstructure Simulation and Constitutive Modelling of Magnetorheological Fluids Based on the Hexagonal Close-packed Structure

Jintao Zhang et al. Materials (Basel). .

Abstract

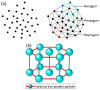
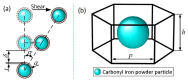
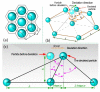
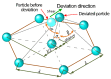
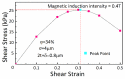
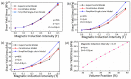
This paper presents a new constitutive model of high particles concentrated magnetorheological fluids (MRFs) that is based on the hexagonal close-packed structure, which can reflect the micro-structures of the particles under the magnetic field. Firstly, the particle dynamic simulations for the forces sustained by carbonyl iron powder (CIP) particles of MRFs are performed in order to investigate the particles chain-forming process at different time nodes. Subsequently, according to the force analyses, a hexagonal close-packed structure, which differs from the existing single-chain structure and body-cantered cubic structure, is adopted to formulate a constitutive model of MRFs with high concentration of the magnetic-responsive particles. Several experiments are performed while considering crucial factors that influence on the chain-forming mechanism and, hence, change the field-dependent shear yield stress in order to validate the proposed model. These factors include the magnetic induction intensity, volume fraction and radius of CIP particles, and surfactant coating thickness. It is shown that the proposed modeling approach can predict the field-dependent shear yield stress much better than the single-chain model. In addition, it is identified that the shear yield stress is increased as the particle volume fraction increases and surfactant coating thickness decreases. It is believed that the proposed constitutive model can be effectively used to estimate the field-dependent shear yield stress of MRFs with a high concentration of iron particles.

Keywords: constitutive modeling; hexagonal close-packed structure; magnetorheological fluids; microstructure; particle dynamics analysis.

PubMed Disclaimer

Conflict of interest statement

The authors declare no conflict of interest.

Figures

Figure 1
Figure 1
The three-dimensional distribution of the chain-forming process of magnetorheological fluid (MRF) at (a) 0 ms, (b) 0.41 ms, (c) 1 ms and (d) 1.68 ms under the magnetic field.
Figure 2
Figure 2
(a) The schematic of MRF microstructure perpendicular to magnetic field; (b) The schematic of the hexagonal close-packed structure.
Figure 3
Figure 3
(a) The deviation angle of magnetic dipoles under shear in a single chain; (b) The space occupied by one single CIP particle.
Figure 4
Figure 4
(a) The overall structure for the close-packed unit particles; (b) Angles between the offset magnetic dipole i and the contiguous magnetic dipoles in the vertical direction; and, (c) Angles between the front and rear magnetic dipoles and the offset magnetic dipole along shear direction.
Figure 5
Figure 5
Angles between the magnetic dipoles on both sides and the offset magnetic dipole along shear direction.
Figure 6
Figure 6
Shear stress-strain curve.
Figure 7
Figure 7
(a) Fitting diagram of shear yield stress and magnetic induction intensity relationship of known model. (φ = 25%); (b) and (c) Result of shear yield stress and magnetic induction intensity relationship of unknown model; and, (d) Result of shear yield stress and CIP volume fraction.
Figure 8
Figure 8
(a) Result of MRF shear yield stress of and CIP radius; (b) Result of shear yield stress and the surfactant coating thickness.
See this image and copyright information in PMC

References

    1. Wang S.Y., Song W.L., Li H.L., Wang N. Modeling and multi-field simulation annlysis of a multi-cylindrical magneto-rheological brake. Int. J. Appl. Electrom. 2018;57:399–414. doi: 10.3233/JAE-170149. - DOI
    1. Qi S., Guo H.Y., Chen J., Fu J., Hu C.G., Yu M., Wang Z.L. Magnetorheological elastomers enabled high-sensitive self-powered tribo-sensor for magnetic field detection. Nanoscale. 2018;10:4745–4752. doi: 10.1039/C7NR09129J. - DOI - PubMed
    1. Zhang J.Q., Zhang J., Kong Y.N., Gao Y.Q., Jia J.F., Wang H.T. Summarization of magnetorheological fluid and its application. J. Acad. Armored Force Eng. 2010;24:5–10. doi: 10.1016/j.jmaa.2010.03.038. - DOI
    1. Fu J., Bai J.F., Lai J.J., Li P.D., Yu M., Lam H.K. Adaptive fuzzy control of a magnetorheological elastomer vibration isolation system with time-varying sinusoidal excitations. J. Sound Vib. 2019;456:386–406. doi: 10.1016/j.jsv.2019.05.046. - DOI
    1. Brigadnov I.A., Dorfmann A. Mathematical modeling of magnetorheological fluids. Continuum Mech. Thermodyn. 2005;17:29–42. doi: 10.1007/s00161-004-0185-1. - DOI

LinkOut - more resources