Application of the Finite Element Method in the Analysis of Composite Materials: A Review
- PMID: 32260389
- PMCID: PMC7240738
- DOI: 10.3390/polym12040818
Application of the Finite Element Method in the Analysis of Composite Materials: A Review
Abstract
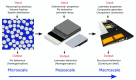
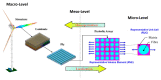
The use of composite materials in several sectors, such as aeronautics and automotive, has been gaining distinction in recent years. However, due to their high costs, as well as unique characteristics, consequences of their heterogeneity, they present challenging gaps to be studied. As a result, the finite element method has been used as a way to analyze composite materials subjected to the most distinctive situations. Therefore, this work aims to approach the modeling of composite materials, focusing on material properties, failure criteria, types of elements and main application sectors. From the modeling point of view, different levels of modeling-micro, meso and macro, are presented. Regarding properties, different mechanical characteristics, theories and constitutive relationships involved to model these materials are presented. The text also discusses the types of elements most commonly used to simulate composites, which are solids, peel, plate and cohesive, as well as the various failure criteria developed and used for the simulation of these materials. In addition, the present article lists the main industrial sectors in which composite material simulation is used, and their gains from it, including aeronautics, aerospace, automotive, naval, energy, civil, sports, manufacturing and even electronics.
Keywords: anisotropic material; failure criteria; multiscale approaches; orthotropic material; plate element; shell element; transverse isotropic material.
Conflict of interest statement
The authors declare no conflict of interest.
Figures
















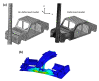

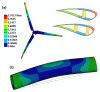

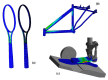


References
-
- Rezende M.C., Costa M.L., Botelho E.C. Compósitos Estruturais: Tecnologia e Prática. 1st ed. Artliber; São Paulo, Brazil: 2011.
-
- Callister Junior W.D., Rethwisch D.G. Materials Science and Engineering: An. Introduction. 8th ed. LTC; São Paulo, Brazil: 2013.
-
- Kaw A.K. Mechanics of Composite Materials. 2nd ed. Taylor & Francis; Boca Raton, FL, USA: 2006.
-
- Durand L.P., editor. Composite Materials Research Progress. 1st ed. Nova Science Publishers, Inc.; New York, NY, USA: 2008.
-
- Chung D.D.L. Engineering Materials and Processes. 2nd ed. Springer; London, UK: 2010. Composite Materials.
Publication types
Grants and funding
LinkOut - more resources
Full Text Sources
Research Materials

