New Insights into Folding, Misfolding, and Nonfolding Dynamics of a WW Domain

Abstract

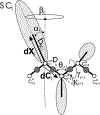
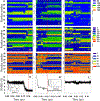
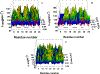
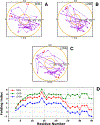
Intermediate states in protein folding are associated with formation of amyloid fibrils, which are responsible for a number of neurodegenerative diseases. Therefore, prevention of the aggregation of folding intermediates is one of the most important problems to overcome. Recently, we studied the origins and prevention of formation of intermediate states with the example of the Formin binding protein 28 (FBP28) WW domain. We demonstrated that the replacement of Leu26 by Asp26 or Trp26 (in ∼15% of the folding trajectories) can alter the folding scenario from three-state folding, a major folding scenario for the FBP28 WW domain (WT) and its mutants, toward two-state or downhill folding at temperatures below the melting point. Here, for a better understanding of the physics of the formation/elimination of intermediates, (i) the dynamics and energetics of formation of β-strands in folding, misfolding, and nonfolding trajectories of these mutants (L26D and L26W) is investigated; (ii) the experimental structures of WT, L26D, and L26W are analyzed in terms of a kink (heteroclinic standing wave solution) of a generalized discrete nonlinear Schrödinger equation. We show that the formation of each β-strand in folding trajectories is accompanied by the emergence of kinks in internal coordinate space as well as a decrease in local free energy. In particular, the decrease in downhill folding trajectory is ∼7 kcal/mol, while it varies between 31 and 48 kcal/mol for the three-state folding trajectory. The kink analyses of the experimental structures give new insights into formation of intermediates, which may become a useful tool for preventing aggregation.

Figure 1.

Amino acid sequence of the triple β-strand WW domain from the Formin binding protein 28 (FBP28) (1E0L) (panel A), and experimental NMR-derived structure of 1E0L (panel B). The mutated residue is highlighted in red color (panel A) and represented by sphere (panel B). Residues forming the β-strands are highlighted in yellow color.

Figure 2.

The UNRES model of polypeptide chains. The interaction sites are peptide-bond centers (p), and side-chain ellipsoids of different sizes (SC) attached to the corresponding α-carbons with different “bond lengths”, b_SC. The α-carbon atoms are represented by small open circles. The equilibrium distance of the C^α…C^α virtual bonds is taken as 3.8 Å, which corresponds to planar trans peptide groups. The geometry of the chain can be described either by the virtual-bond vectors dC_i (C^α_i…C^α_i+1), i = 1, 2,…, N - 1 and dX_i (C^α_i…SC_i), i = 2, 3,…, N - 1 (represented by thick dashed arrows), where N is the number of residues, or in terms of virtual-bond lengths, backbone virtual-bond angles θ_i, i = 2, 3,…, N - 1, backbone virtual-bond-dihedral angles γ_i, i = 2, 3,…, N - 2, and the angles α_i and β_i, i = 2, 3,…, N - 1 that describe the location of a side chain with respect to the coordinate frame defined by C^α_i-1, C^α_i and C^α_i+1. The angles κ_i used here are complements of the θ_i angles, i.e., π − θ_i.

Figure 3.

Filled contour plots of the backbone virtual-bond angles θ (in degree) (panels A, E, I), backbone virtual-bond-dihedral angles γ (in degree) (panels B, F, J), and local free energies (in kcal/mol) (panels C, G, K) vs time for three-state folding trajectory of L26D mutant (panels A – C), downhill folding trajectory of L26W mutant (panels E – G), and nonfolding trajectory of L26D mutant (panels I – K). The vertical black lines on each panel correspond to the β-strand regions. The root-mean-square deviations (RMSDs) vs time for three-state folding, downhill folding, and nonfolding trajectory are presented in panels D, H and L, respectively. The insets in panels D and H represent the free-energy profiles (in kcal/mol) as functions of RMSD. Vertical red dashed lines indicate the folding time of L26D and L26W.

Figure 4.

The UNRES energy change during the formation of the first, second and third β-strands for three-state folding trajectory of L26D mutant (panels A-C), downhill folding trajectory of L26W mutant (panels D-F), and nonfolding trajectory of L26D mutant (panels G-I).

Figure 5.

3-D representation of the backbone virtual-bond angles θ vs time for three-state folding trajectory of L26D mutant (panel A), downhill folding trajectory of L26W mutant (panel B), and nonfolding trajectory of L26D mutant (panel C). The NMR-derived structural data (red curves on panels A and B) are computed from the first model of the PDB ID codes 2N4R (L26D) and 2N4T (L26W). The horizontal black lines on panels A and B correspond to the β-strand regions.

Figure 6.

The first five principal components of three-state folding trajectory of L26D mutant (panels A-E), downhill folding trajectory of L26W mutant (panels F-J), and nonfolding trajectory of L26D mutant (panels K-O). The insets in panels A-E represent free-energy profiles of the corresponding principal components for the entire three-state folding trajectory (~ 1.4 μs).

Figure 7.

The comparison of experimental and calculated angle spectra of three selected structures for the FBP28 WW domain (left panels), L26D (middle panels) and L26W (right panels) in terms of virtual-bond κ_i (experimental-red, calculated-blue) and torsion γ_i (experimental-green, calculated-yellow) values.

Figure 8.

Top panels of A, B and C represent experimental values of the virtual-bond κ_i (red) and torsion γ_i (blue) angle spectra of 1E0L (panel A), 2N4R (panel B) and 2N4T (panel C). Remaining three panels in A, B and C illustrate kink structures, i.e., the virtual-bond κ_i (red) and torsion γ_i (green) angle spectra for three selected structures of 1E0L (panel A), 2N4R (panel B) and 2N4T (panel C), after ℤ₂ gauge transformation (eq. 8) was made. Blue circles represent centers of kinks, purple rhombuses represent the right edges of left kinks.

Figure 8.

Top panels of A, B and C represent experimental values of the virtual-bond κ_i (red) and torsion γ_i (blue) angle spectra of 1E0L (panel A), 2N4R (panel B) and 2N4T (panel C). Remaining three panels in A, B and C illustrate kink structures, i.e., the virtual-bond κ_i (red) and torsion γ_i (green) angle spectra for three selected structures of 1E0L (panel A), 2N4R (panel B) and 2N4T (panel C), after ℤ₂ gauge transformation (eq. 8) was made. Blue circles represent centers of kinks, purple rhombuses represent the right edges of left kinks.

Figure 8.

Top panels of A, B and C represent experimental values of the virtual-bond κ_i (red) and torsion γ_i (blue) angle spectra of 1E0L (panel A), 2N4R (panel B) and 2N4T (panel C). Remaining three panels in A, B and C illustrate kink structures, i.e., the virtual-bond κ_i (red) and torsion γ_i (green) angle spectra for three selected structures of 1E0L (panel A), 2N4R (panel B) and 2N4T (panel C), after ℤ₂ gauge transformation (eq. 8) was made. Blue circles represent centers of kinks, purple rhombuses represent the right edges of left kinks.

Figure 9.

The folding index trajectories for the FBP28 WW domain (A), L26D (B), and L26W (C), and the folding index for the FBP28 WW domain, L26D and L26W (D).