Confidence controls perceptual evidence accumulation

Abstract

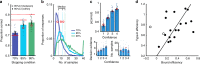
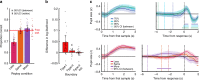
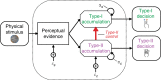
Perceptual decisions are accompanied by feelings of confidence that reflect the likelihood that the decision was correct. Here we aim to clarify the relationship between perception and confidence by studying the same perceptual task across three different confidence contexts. Human observers were asked to categorize the source of sequentially presented visual stimuli. Each additional stimulus provided evidence for making more accurate perceptual decisions, and better confidence judgements. We show that observers' ability to set appropriate evidence accumulation bounds for perceptual decisions is strongly predictive of their ability to make accurate confidence judgements. When observers were not permitted to control their exposure to evidence, they imposed covert bounds on their perceptual decisions but not on their confidence decisions. This partial dissociation between decision processes is reflected in behaviour and pupil dilation. Together, these findings suggest a confidence-regulated accumulation-to-bound process that controls perceptual decision-making even in the absence of explicit speed-accuracy trade-offs.

Fig. 1. Procedure.

On each trial, observers were shown a series of oriented Gabors and had to determine which distribution the orientations were drawn from. a The orientations were drawn from one of two circular Gaussian (von-Mises) distributions centred on −45° (blue) and + 45° (orange) relative to vertical (0°). The distributions were overlapping such that a stimulus oriented 45° from vertical is most likely to have been drawn from the orange distribution (orange arrow) but still could have been drawn from the blue distribution (blue arrow). b The experiment involved two sessions. In session 1, observers completed the Stopping task. On each trial of the Stopping task the series of stimuli continued until observers entered a Type-I response: blue or orange distribution. They were asked to enter their response when they felt they had a certain probability of being correct. The three target performance levels (70%, 85% and 90% correct) were completed in separate blocks. In session 2, observers completed the Free task followed by the Replay task. The Free task was the same as the Stopping task, except observers were asked to enter their response when they felt ready (after p samples). In the Replay task, observers entered their Type-I response once cued (fixation changing to red). They then gave a Type-II response: a rating (1 to 4) of how confident they were that they were correct. Unbeknownst to observers, the Replay task actually replayed the exact same trials from the Free task, except the number of samples was either the same as they had chosen to respond to (x = p), two fewer (x = p − 2), or four additional samples (x = p + 4). These trials comprise the Same, Less and More conditions, respectively. Across all tasks, the fixation point (black dot) and colour guide were present throughout each trial. The samples were presented at a rate of 4 Hz, with 200 ms of stimulus presence (including 25 ms ramp at onset and offset) and 50 ms inter-stimulus interval. All tasks consisted of repetitions of the same 100 trials pre-defined for each observer.

Fig. 2. Computational model and simulations.

a On each trial, the observer sums the decision evidence (z) of each sample, n, which is the log-probability of the orientation, given the distribution $\left({\ell }_n\right)$, corrupted by additive i.i.d. Gaussian noise (ε_n, with standard deviation σ), and weighted according to the observer’s leak (v_n, an exponential function of α). Three example trials are shown from each distribution (blue and orange traces, with the shading representing the variability due to noise). Evidence accumulation stops once the evidence reaches the bound, in this case a collapsing bound defined by Λ_n, shown by the black curves. b Participant proportion correct against the simulated data based on the fitted parameters of the computational model, for each participant in each condition of the Stopping task (70%, 85% and 90% correct in blue, cyan and green, respectively). The diagonal shows equality. Red arrows mark the performance targets. c The same as b for the median number of samples the observer chose to respond to.

Fig. 3. The relationship between Type-I bound efficiency and Type-II efficiency.

a Average proportion correct in each condition of the Stopping task. The horizontal red lines subtend the target performance level in each condition. Error bars show 95% within-subjects (thick) and between-subjects (thin) confidence intervals n = 20. The red circles show the predicted performance based on the fitted parameters of the model. b Average proportion of trials by the number of samples the observers chose to respond to in each condition of the Stopping task. Vertical dashed lines show the average median number of samples. Red circles show the predicted median number of samples based on the fitted parameters of the model. c Proportion correct (top), decision evidence (bottom left) and number of samples (bottom right) by confidence rating in the Replay task. Error bars show 95% within-subjects confidence intervals (n = 20), and red circles show the predicted performance at each confidence level based on the fitted parameters of the model. d Each observer’s bound efficiency (x-axis) by their Type-II efficiency (y-axis) and the line minimising the perpendicular distance from these points, here shown excluding two outlier participants (open circles) whose optimal bound was estimated using maximum performance rather than 85% correct (y = 1.5× + 0.2, p-value for slope = 0.026, one-sided, based on bootstrapping, with outlier participants removed).

Fig. 4. Evidence for a covert bound on Type-I evidence accumulation.

a Average proportion correct in each condition of the Replay task. In the Same condition (orange), observers were shown the same number of samples as they had chosen to respond to in the Free task, in the Less condition (magenta) they were shown two fewer samples, and in the More condition (purple), four additional samples. The red horizontal line shows the average proportion correct in the Free task, where the exact same trials were shown (with the exception of the condition manipulation). Error bars show 95% within-subject (thick) and between-subject (thin) confidence intervals (n = 20). Open red circles show the model predictions based on simulations of the bounded model. b Difference in log-likelihood (relative improvement in fit) between the model fit with a covert boundary compared to the model without. The bars show the improvement in the fit to Type-I responses with a bound on Type-I evidence accumulation (labelled Type-I), the improvement in the fit to Type-II responses when the Type-II is bounded at the same time as the Type-I evidence (labelled Type-II), and the improvement in the fit to Type-II responses when an independent bound is fit to the accumulation of Type-II evidence (labelled Type-II ind.). Error bars show 95% between-subject confidence intervals n = 20. c Standardised pupil size in the Stopping task (top) and Replay task (bottom), averaged across time-windows aligned to the start of each trial (left) and to the response (right). Shading shows 95% between-subjects confidence intervals (n = 19). Trial-start aligned data were baselined to the average at time 0, response-aligned data were baselined to the average prior to trial start (−4 to −3 s in the Stopping task, and −6 to −5 s in the Replay task). Black vertical lines in the trial-start plots show the timing of the 2nd and 3rd samples. Vertical lines in the response plots show the average median timing of the start of the trial. Differences from baseline in the response-aligned epochs were tested using two-sided Wilcoxon sign rank tests, with significant clusters shown with horizontal lines (corrected p < 0.05).

Fig. 5. The accumulation of evidence for Type-I and Type-II decisions.

The dashed box encloses the hidden decision processes, which determine the relationship between the observable variables (the physical input and behavioural output). Information from the physical stimulus is transformed into decision evidence, which is accumulated for the Type-I decision with additive Gaussian noise (ε_s) and weighted according to the leak (α_s). Evidence accumulated for the Type-II decision incurs additional noise (ε_c) and a separate leak (α_c). Type-II control is exerted on the Type-I evidence accumulation process, depicted by the red arrow, where the accumulated evidence is sent to the decision output once the boundary is reached, based on the Type-II evidence. The Type-II evidence may continue to accumulate even after the boundary has been reached.

Fig. 6. Pupil response to confidence and boundary crossing.

Average standardised pupil size in the Replay task across response-aligned (dashed vertical black line) time-windows, baselined to the average over −5 to −4 s. Shaded error bars show the 95% within-subjects confidence intervals. Differences between these lines were assessed using Wilcoxon sign rank tests, with significant clusters shown in the horizontal lines at the bottom of each plot. a Trials separated by confidence rating (high = 3 and 4, low = 1 and 2), with the black horizontal line showing significant differences. b Trials separated by whether it was likely that the observer’s covert bound was crossed, based on the fitted parameters of the computational model, with the black horizontal line showing significant differences. c Average change in pupil size from the time of the response to 1 s after the response for low- and high-confidence trials within crossed (red dashed) and not crossed (black) trials. Error bars show 95% within-subjects CI. d Time of peak pupil size in the low- and high-confidence trials within crossed (red dashed) and not crossed (black) trials.