Minimum epistasis interpolation for sequence-function relationships

Abstract

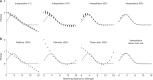
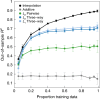
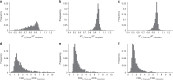
Massively parallel phenotyping assays have provided unprecedented insight into how multiple mutations combine to determine biological function. While such assays can measure phenotypes for thousands to millions of genotypes in a single experiment, in practice these measurements are not exhaustive, so that there is a need for techniques to impute values for genotypes whose phenotypes have not been directly assayed. Here, we present an imputation method based on inferring the least epistatic possible sequence-function relationship compatible with the data. In particular, we infer the reconstruction where mutational effects change as little as possible across adjacent genetic backgrounds. The resulting models can capture complex higher-order genetic interactions near the data, but approach additivity where data is sparse or absent. We apply the method to high-throughput transcription factor binding assays and use it to explore a fitness landscape for protein G.

Fig. 1. Minimizing average local epistasis.

a The classical epistatic coefficient ϵ measures the difference in the effect of a mutation between two adjacent genetic backgrounds. Here ϵ is shown as the difference between the effect of an a → A mutation on a B versus b background. b Larger spaces of genotypes can be decomposed into faces consisting of a wild-type sequence, two single mutants and a double mutant; one such face is highlighted in gray. For each face, we quantify epistasis locally by calculating the corresponding value of ϵ². We then quantify the total amount of epistasis for the sequence–function relationship by taking the average of these values across all faces, $\overline{{ϵ}^2}$. By assigning phenotypic values for the out-of-sample genotypes that minimize $\overline{{ϵ}^2}$, we infer the least epistatic sequence–function relationship compatible with the data in the sense that the average squared difference in the effects of mutations between adjacent genetic backgrounds is as small as possible.

Fig. 2. Minimum epistasis interpolation but not low-order regression models can learn the crater model for transcriptional regulation.

The crater model produces a fitness landscape where fitness depends only on the Hamming distance to the wild-type sequence, with an optimum at an intermediate Hamming distance (l = 16 and α = 2; see “Methods” for other parameters). Gray curve shows the true fitness landscape. a Out-of-sample predictions of minimum epistasis interpolation with random subsets of 1%, 10%, 50%, and 90% of genotypes used for training. The predictions adapt to the shape of the crater landscape with increasing data density. For each distance class, at least one genotype was assigned to the test set to ensure an informative visualization of model fits. b Reconstruction of the crater landscape by the additive, pairwise, and three-way regression models fitted using ordinary least squares with 100% of the data. The interpolation panel shows leave-one-out results (equivalent to applying the smoother M to the full landscape).

Fig. 3. Model performance for the simulated sparse random interaction landscape with all orders of epistasis (l = 7, α = 4).

L₂-regularized pairwise and three-way regression models and L₁-regularized three-way model were fit with regularization parameters chosen by 10-fold cross-validation. Predictive power (out-of-sample R²) is plotted as a function of the proportion of in-sample genotypes assigned as the training data. Error bars indicate one standard error around the mean, n = 3.

Fig. 4. Model performance for the GB1 combinatorial mutagenesis data set. Additive models were fit using ordinary least squares.

Pairwise and three-way interaction models were fit using regularized regression with regularization parameters chosen by tenfold cross-validation (see “Methods”). Points are color-coded to represent the proportion of the data randomly assigned as training. Error bars indicate one standard error around the mean. n = 3. a Predictive power (out-of-sample R²) as a function of the proportion of in-sample genotypes. b Mean-squared epistasis coefficients between random pairs of mutations connecting out-of-sample genotypes as a function of the proportion of in-sample genotypes. c Behavior across all of sequence space (both in-sample and out-of-sample) of the five models assessed using R² between the fitted model and the complete data set (total R²) and average local epistasis ($\overline{{ϵ}^2}$). Each model is represented by a curve with points corresponding to increasing proportion of the total data set assigned as training data. Note that the additive model appears at the lower left part of the plot as its total R² quickly stabilizes and its $\overline{{ϵ}^2}$ is zero by definition. d The number of local maxima of the reconstructed landscapes at different training data sizes. e Model optimism assessed by plotting in-sample R² vs. out-of-sample R².

Fig. 5. Visualization of the GB1 landscape reconstructed using minimum epistasis interpolation and the local nonepistatic smoother.

Genotypes are plotted using the dimensionality reduction technique from ref. (see “Methods”). Points are genotypes, colored according to their smoothed binding phenotype, and two genotypes are connected by an edge if they differ by a single amino acid substitution. Local fitness peaks are highlighted by black circles. The x- and y-axis are, respectively, the first and second diffusion coordinate and have units of square-root expected neutral substitutions per site. Three high-fitness regions are characterized by their distinct sequence composition (sequence logos, see Supplementary Fig. 5b for numerical values). The scatter plots show the fit of an additive model to the unsmoothed binding values within each of the three high-binding regions. These scatter plots indicate that, despite the complex pattern of epistasis in the landscape as a whole, the sequence–function relationship is approximately additive within each individual high-binding region.

Fig. 6. Model comparison using protein-binding microarray data from 1121 transcription factors.

For each TF, 80% of sequences were randomly assigned as training data. L₂-regularized pairwise regression, L₂-regularized three-way regression, and L₁-regularized three-way regression were fit with regularization parameter chosen by cross-validation. For each TF, we calculate the out-of-sample R² and false discovery rate (FDR) defined as the frequency that an out-of-sample genotype predicted to be above the 95th percentile of the data were in fact below the 95th percentile. a–c Histograms of the ratios of R² of the regression models and minimum epistasis interpolation. d–f Histograms of the ratios of the false discovery rate of the regression models and minimum epistasis interpolation.