Investigation of epidemic spreading process on multiplex networks by incorporating fatal properties
- PMID: 32287502
- PMCID: PMC7112296
- DOI: 10.1016/j.amc.2019.02.049
Investigation of epidemic spreading process on multiplex networks by incorporating fatal properties
Abstract
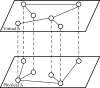
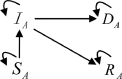
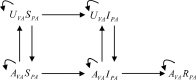
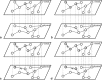
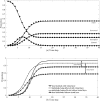
Numerous efforts have been devoted to investigating the network activities and dynamics of isolated networks. Nevertheless, in practice, most complex networks might be interconnected with each other (due to the existence of common components) and exhibit layered properties while the connections on different layers represent various relationships. These types of networks are characterized as multiplex networks. A two-layered multiplex network model (usually composed of a virtual layer sustaining unaware-aware-unaware (UAU) dynamics and a physical one supporting susceptible-infected-recovered-dead (SIRD) process) is presented to investigate the spreading property of fatal epidemics in this manuscript. Due to the incorporation of the virtual layer, the recovered and dead individuals seem to play different roles in affecting the epidemic spreading process. In details, the corresponding nodes on the virtual layer for the recovered individuals are capable of transmitting information to other individuals, while the corresponding nodes for the dead individuals (which are to be eliminated) on the virtual layer should be removed as well. With the coupled UAU-SIRD model, the relationships between the focused variables and parameters of the epidemic are studied thoroughly. As indicated by the results, the range of affected individuals will be reduced by a large amount with the incorporation of virtual layers. Furthermore, the effects of recovery time on the epidemic spreading process are also investigated aiming to consider various physical conditions. Theoretical analyses are also derived for scenarios with and without required time periods for recovery which validates the reducing effects of incorporating virtual layers on the epidemic spreading process.
Keywords: Epidemic information spreading; Multiplex networks; Theoretical validation; UAU-SIRD model.
© 2019 Published by Elsevier Inc.
Figures
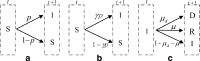
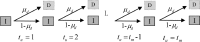




References
-
- Barrat A., Barthelemy M., Vespignani A. Dynamical Processes on Complex Networks. Cambridge University Press; 2008.
-
- Wang Z., Bauch C.T., Bhattacharyya S., d’Onofrio A., Manfredi P., Perc M., Perra N., Salathé M., Zhao D. Stat. Phys. Vaccin. Phys. Rep. 2016;664:1–113.
-
- Boccaletti S., Latora V., Moreno Y., Chavez M., Hwang D.-U. Complex networks: structure and dynamics. Phys. Rep. 2006;424(4–5):175–308.
LinkOut - more resources
Full Text Sources
Research Materials
