Why is it difficult to accurately predict the COVID-19 epidemic?
- PMID: 32289100
- PMCID: PMC7104073
- DOI: 10.1016/j.idm.2020.03.001
Why is it difficult to accurately predict the COVID-19 epidemic?
Abstract
Since the COVID-19 outbreak in Wuhan City in December of 2019, numerous model predictions on the COVID-19 epidemics in Wuhan and other parts of China have been reported. These model predictions have shown a wide range of variations. In our study, we demonstrate that nonidentifiability in model calibrations using the confirmed-case data is the main reason for such wide variations. Using the Akaike Information Criterion (AIC) for model selection, we show that an SIR model performs much better than an SEIR model in representing the information contained in the confirmed-case data. This indicates that predictions using more complex models may not be more reliable compared to using a simpler model. We present our model predictions for the COVID-19 epidemic in Wuhan after the lockdown and quarantine of the city on January 23, 2020. We also report our results of modeling the impacts of the strict quarantine measures undertaken in the city after February 7 on the time course of the epidemic, and modeling the potential of a second outbreak after the return-to-work in the city.
Keywords: Bayesian inference; COVID-19 epidemic in Wuhan; Model selection; Nonidentifiability; Peak time of epidemic; Quarantine; SIR and SEIR models.
© 2020 The Authors.
Conflict of interest statement
The authors claim no conflict of interests.
Figures

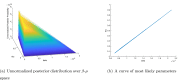
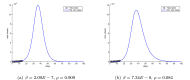
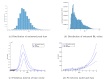
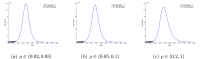
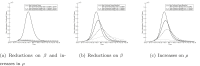
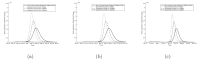
References
-
- Akaike H. Second international symposium on information theory. Akademiai Kiado; Budapest: 1973. Information theory and an extension of the maximum likelihood principle; pp. 267–281.
-
- Burnham K., Anderson D. Springer-Verlag; New York: 2002. Model selection and multimodel inference: A practical information-theoretic approach.
-
- Chen M., Shao Q., Ibrahim J. Springer-Verlag; New York: 2000. Monte Carlo methods in bayesian computation.
LinkOut - more resources
Full Text Sources
Molecular Biology Databases

