Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2020 Apr 24;13(8):1979.
doi: 10.3390/ma13081979.

Dislocation Density Based Flow Stress Model Applied to the PFEM Simulation of Orthogonal Cutting Processes of Ti-6Al-4V

Juan Manuel Rodríguez  1 , Simon Larsson  2 , Josep Maria Carbonell  3   4 , Pär Jonsén  2
Affiliations

Dislocation Density Based Flow Stress Model Applied to the PFEM Simulation of Orthogonal Cutting Processes of Ti-6Al-4V

Juan Manuel Rodríguez et al. Materials (Basel). .

Abstract

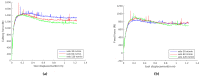
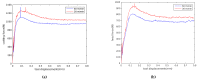
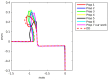
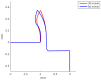
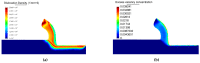
Machining of metals is an essential operation in the manufacturing industry. Chip formation in metal cutting is associated with large plastic strains, large deformations, high strain rates and high temperatures, mainly located in the primary and in the secondary shear zones. During the last decades, there has been significant progress in numerical methods and constitutive modeling for machining operations. In this work, the Particle Finite Element Method (PFEM) together with a dislocation density (DD) constitutive model are introduced to simulate the machining of Ti-6Al-4V. The work includes a study of two constitutive models for the titanium material, the physically based plasticity DD model and the phenomenology based Johnson-Cook model. Both constitutive models were implemented into an in-house PFEM software and setup to simulate deformation behaviour of titanium Ti6Al4V during an orthogonal cutting process. Validation show that numerical and experimental results are in agreement for different cutting speeds and feeds. The dislocation density model, although it needs more thorough calibration, shows an excellent match with the results. This paper shows that the combination of PFEM together with a dislocation density constitutive model is an excellent candidate for future numerical simulations of mechanical cutting.

Keywords: Johnson-Cook; Particle Finite Element Method (PFEM); dislocation density constitutive model; metal cutting processes; titanium Ti6Al4V.

PubMed Disclaimer

Conflict of interest statement

The authors declare no conflict of interest.

Figures

Figure 1
Figure 1
Remeshing steps in a standard Particle Finite Element Method (PFEM) numerical simulation.
Figure 2
Figure 2
Three main criteria to remove a particle.
Figure 3
Figure 3
Three main criteria to add a new particle.
Figure 4
Figure 4
Experimental tool; (a) insert, (b) cutting edge profile.
Figure 5
Figure 5
Experimental forces vs. tool displacement for experiment 4 (see Table 5).
Figure 6
Figure 6
Mesh used to create the particles at the beginning of the simulation. Feed 0.05 mm. Dimensions are in mm.
Figure 7
Figure 7
2D plane strain PFEM model of orthogonal cutting: initial set of particles. The picture is for a feed of 0.05 mm.
Figure 8
Figure 8
Particles used at the end of the numerical simulation. The Johnson-Cook constitutive model was used with the parameters with parameters 7.
Figure 9
Figure 9
Predicted forces using the Johnson-Cook model with our parameters 7 (see Table 1); (a) cutting, (b) feed.
Figure 10
Figure 10
Predicted forces using the dislocation density model; (a) cutting, (b) feed.
Figure 11
Figure 11
Predicted chip shape using two constitutive models: dislocation density (DD) and Johnson-Cook. Feed of 0.05 mm and a cutting speed of 60 m/min (Experiment 2).
Figure 12
Figure 12
Predicted chip shape using two constitutive models: dislocation density (DD) and Johnson-Cook. Feed of 0.15 mm and a cutting speed of 60 m/min (Experiment 4).
Figure 13
Figure 13
Predicted chip shape at different cutting speeds using Johnson-Cook model and material properties 7 (see Table 1). Feed of 0.15 mm.
Figure 14
Figure 14
Predicted chip shape at different cutting speeds for the dislocations density model. Feed of 0.15 mm.
Figure 15
Figure 15
Temperature field; (a) the dislocation density, (b) the Johnson-Cook model.
Figure 16
Figure 16
Plastic strain rate; (a) the dislocation density, (b) the Johnson-Cook model.
Figure 17
Figure 17
State variables obtained from the dislocation density (DD) model; (a) dislocation density, (b) vacancy concentration.
See this image and copyright information in PMC

References

    1. Abdulhameed O., Al-Ahmari A., Ameen W., Mian S.H. Additive manufacturing: Challenges, trends, and applications. Adv. Mech. Eng. 2019;11 doi: 10.1177/1687814018822880. - DOI
    1. Ivester R.W., Kennedy M., Davies M., Stevenson R., Thiele J., Furness R., Athavale S. Assesment of machining models: progress report. Mach. Sci. Technol. 2000;4:511–538. doi: 10.1080/10940340008945720. - DOI
    1. Ivester R., Whitenton E., Heigel J., Marusich T., Arthur C. Measuring chip segmentation by high-speed microvideography and comparison to finite element modelling simulations; Proceedings of the 10th CIRP International Workshop on Modelling of Machining Operations; Regio Calabria, Italy. 27–28 August 2007; pp. 37–44.
    1. Rakotomalala R., Joyot P., Touratier M. Arbitrary Lagrangian-Eulerian thermomechanical finite-element model of material cutting. Commun. Numer. Methods Eng. 1993;9:975–987. doi: 10.1002/cnm.1640091205. - DOI
    1. Sekhon G., Chenot J. Numerical Simulation of continuos chip formation during non-steady orthogonal cutting. Eng. Computat. 1993;10:31–48. doi: 10.1108/eb023893. - DOI

LinkOut - more resources