Predicting Concussion Outcome by Integrating Finite Element Modeling and Network Analysis

Abstract

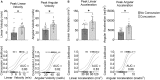
Concussion is a significant public health problem affecting 1.6-2.4 million Americans annually. An alternative to reducing the burden of concussion is to reduce its incidence with improved protective equipment and injury mitigation systems. Finite element (FE) models of the brain response to blunt trauma are often used to estimate injury potential and can lead to improved helmet designs. However, these models have yet to incorporate how the patterns of brain connectivity disruption after impact affects the relay of information in the injured brain. Furthermore, FE brain models typically do not consider the differences in individual brain structural connectivities and their purported role in concussion risk. Here, we use graph theory techniques to integrate brain deformations predicted from FE modeling with measurements of network efficiency to identify brain regions whose connectivity characteristics may influence concussion risk. We computed maximum principal strain in 129 brain regions using head kinematics measured from 53 professional football impact reconstructions that included concussive and non-concussive cases. In parallel, using diffusion spectrum imaging data from 30 healthy subjects, we simulated structural lesioning of each of the same 129 brain regions. We simulated lesioning by removing each region one at a time along with all its connections. In turn, we computed the resultant change in global efficiency to identify regions important for network communication. We found that brain regions that deformed the most during an impact did not overlap with regions most important for network communication (Pearson's correlation, ρ = 0.07; p = 0.45). Despite this dissimilarity, we found that predicting concussion incidence was equally accurate when considering either areas of high strain or of high importance to global efficiency. Interestingly, accuracy for concussion prediction varied considerably across the 30 healthy connectomes. These results suggest that individual network structure is an important confounding variable in concussion prediction and that further investigation of its role may improve concussion prediction and lead to the development of more effective protective equipment.

Keywords: biomechanics; concussion; graph theory; networks; structural connectivity.

Figure 1

Overview of methods. (A) Sanchez et al. estimated the 6 degree-of-freedom kinematics of 53 NFL impact reconstructions and then used them as inputs into a three-dimensional finite element (FE) model developed by Wu et al. (2019b) to estimate the regional maximum principal strain (rMPS) in each of 129 brain regions (Sanchez et al., 2019). Image taken from Sanchez et al. (2019) with permission. (B) Betzel et al. parcellated diffusion spectrum imaging from 30 healthy subjects to construct an adjacency matrix representing the structural connectivity between 129 brain regions (Betzel et al., 2016). We performed nodal deletions and then calculated the resultant change in global efficiency (GE). Panel (C) is a schematic depicting the equations used for calculating GE itself, the network effects of a simulated single node deletion, and the equation used to calculate the resultant change in GE. (D) We ranked the brain regions based on their rMPS and ΔGE. Note that ΔGE is an average of all 30 healthy subject's unique ΔGEs. We reordered the regional rMPSs to match the high rMPS and high ΔGE rankings. Note again that each subject has its own reordered rMPS ranking based on differential ΔGE. We then considered n = 1 to 4 regions' rMPS in our multivariate logistic regression, adding rMPSs in order based on the High rMPS Ranking or High ΔGE ranking.

Figure 2

Peak kinematics delineate concussion outcomes. (A) Impact velocity is different for concussive vs. non-concussive impacts for peak linear velocity and peak angular velocity. The AUC-testing of the ROC curve for the logistic regression for peak linear velocity was 0.80 and for peak angular velocity was 0.82. (B) Impact acceleration is different for concussive vs. non-concussive impacts for peak linear acceleration and peak angular acceleration. The AUC of the ROC curve for the logistic regression for peak linear acceleration was 0.83 and for peak angular acceleration was 0.88. *Indicates significance at the α = 0.05 level; Wilcoxon Rank-Sum Test. Dashed line indicates 95% confidence interval.

Figure 3

Global 95th Percentile MPS (MPS95) delineates concussion outcomes. (A) MPS95 is significantly different for concussion vs. no concussion cases (p = 7.24e-06; Wilcoxon Rank-Sum Test). (B,C) Univariate logistic regression using MPS95 produces an AUC-testing of 0.85. *Indicates significance at the α = 0.05 level; Wilcoxon Rank-Sum Test.

Figure 4

Regional MPS (rMPS) is significantly different for no concussion vs. concussion cases. rMPS is significantly different in concussion vs. no concussion impact cases in 102 regions (*p < 0.05, Wilcoxon Rank-Sum Test with Bonferroni Correction for n = 129 comparisons). Error bars represent standard deviation across 20 concussion cases and 33 no concussion cases.

Figure 5

Change in global efficiency after regional deletion is consistent across number of regions deleted. Average change in global efficiency after deletion of one (A), two (B), and three (C) brain regions at a time.

Figure 6

High rMPS and high average ΔGE rMPS are similarly accurate, but there are large differences when considering individual brain architectures. (A) The rMPSes corresponding to the High rMPS Regions and the High ΔGE Regions were used for Multivariate Logistic Regression using either 1, 2, 3, or 4 regions at a time. (B) When considering the rMPS in multiple regions for logistic regression, adding regions based on ΔGE ranking produced qualitatively similar results compared to adding regions based on High rMPS ranking. (C) When considering the individual ΔGE rankings for the 30 healthy subjects, there was considerable variability – up to a 0.12 difference in validation accuracy depending on how many regions' rMPS were considered.