Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2020 Sep:88:105303.
doi: 10.1016/j.cnsns.2020.105303. Epub 2020 Apr 30.

Mathematical modeling of the spread of the coronavirus disease 2019 (COVID-19) taking into account the undetected infections. The case of China

B Ivorra  1 , M R Ferrández  2 , M Vela-Pérez  1 , A M Ramos  1
Affiliations

Mathematical modeling of the spread of the coronavirus disease 2019 (COVID-19) taking into account the undetected infections. The case of China

B Ivorra et al. Commun Nonlinear Sci Numer Simul. 2020 Sep.

Abstract

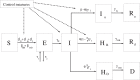
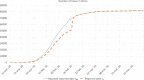
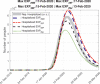
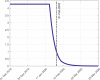
In this paper we develop a mathematical model for the spread of the coronavirus disease 2019 (COVID-19). It is a new θ-SEIHRD model (not a SIR, SEIR or other general purpose model), which takes into account the known special characteristics of this disease, as the existence of infectious undetected cases and the different sanitary and infectiousness conditions of hospitalized people. In particular, it includes a novel approach that considers the fraction θ of detected cases over the real total infected cases, which allows to study the importance of this ratio on the impact of COVID-19. The model is also able to estimate the needs of beds in hospitals. It is complex enough to capture the most important effects, but also simple enough to allow an affordable identification of its parameters, using the data that authorities report on this pandemic. We study the particular case of China (including Chinese Mainland, Macao, Hong-Kong and Taiwan, as done by the World Health Organization in its reports on COVID-19), the country spreading the disease, and use its reported data to identify the model parameters, which can be of interest for estimating the spread of COVID-19 in other countries. We show a good agreement between the reported data and the estimations given by our model. We also study the behavior of the outputs returned by our model when considering incomplete reported data (by truncating them at some dates before and after the peak of daily reported cases). By comparing those results, we can estimate the error produced by the model when identifying the parameters at early stages of the pandemic. Finally, taking into account the advantages of the novelties introduced by our model, we study different scenarios to show how different values of the percentage of detected cases would have changed the global magnitude of COVID-19 in China, which can be of interest for policy makers.

Keywords: COVID-19; Coronavirus; Mathematical model; Numerical simulation; Pandemic; Parameter estimation; SARS-CoV-2; θ-SEIHRD model.

PubMed Disclaimer

Figures

Fig. 1
Fig. 1
Diagram summarizing the model for COVID-19 given by system (1).
Fig. 2
Fig. 2
Diagram summarizing the simplified version of the model for COVID-19 given by system (3).
Fig. 3
Fig. 3
Evolution of the number of cases in China: Reported (cr) and adjusted reported data (car).
Fig. 4
Fig. 4
Evolution of the number of (TOP) cases and (BOTTOM) deaths in China from 1 December 2019 to 29 March 2020: Adjusted reported cases (a.r.c) and deaths, and estimation obtained with EXP29M, EXP25F, EXP08F and EXP29J.
Fig. 5
Fig. 5
Evolution of the number of cases in China from 1 December 2019 to 29 March 2020: Adjusted reported cases (a.r.c.), as well as detected, undetected and total cases obtained with EXP29M.
Fig. 6
Fig. 6
Evolution of the number of Hospitalized (Top) and Recovered (Bottom) people in China from 1 December 2019 to 29 March 2020 considering reported data and estimation obtained with EXP29M.
Fig. 7
Fig. 7
Evolution of the number of Hospitalized people in China from 1 December 2019 to 29 March 2020, considering the adjusted reported cases (a.r.c.) and the results returned at the end of experiments EXP29M, EXP25F, EXP08F and EXP29J.
Fig. 8
Fig. 8
Evolution of the daily number of new people in the exposed compartment (Top-Left), new cases (Top-Right) and new deaths (Bottom) in China from 1 December 2019 to 29 March 2020 considering the results returned at the end of experiment EXP29M. We also report the adjusted daily number of new reported cases and the daily number of new reported deaths.
Fig. 9
Fig. 9
Evolution of the effective reproduction number Re(t) in China from 1 December 2019 to 29 March 2020 obtained with EXP29M.
Fig. 10
Fig. 10
Evolution of the total number of cases (detected plus undetected) in China from 1 December 2019 to 29 March 2020, considering parameters from EXP29M and the function θ given in (8), and also scenarios in which θ(t) is given the constant values of 0.14, 0.25, 0.5, 0.75 and 1.
See this image and copyright information in PMC

References

    1. Anderson M. Population biology of infectious diseases: part 1. Nature. 1979;280:361–367. - PubMed
    1. Ivorra B., Martínez-López B., Sánchez-Vizcaíno J.M., Ramos A.M. Mathematical formulation and validation of the Be-FAST model for classical swine fever virus spread between and within farms. Ann Oper Res. 2014;219(1):25–47.
    1. Martínez-López B., Ivorra B., Ramos A.M., Sánchez-Vizcaíno J.M. A novel spatial and stochastic model to evaluate the within- and between-farm transmission of classical swine fever virus. i. general concepts and description of the model. Vet Microbiol. 2011;147(3–4):300–309. - PubMed
    1. Thieme H.R. Princeton University Press; 2003. Mathematics in population biology. (Mathematical Biology Series).
    1. Brauer F., Castillo-Chávez C. Texts in Applied Mathematics, Springer; 2001. Mathematical Models in Population Biology and Epidemiology.

    2. https://www.springer.com/gp/book/9781441931825.

LinkOut - more resources