Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2020 May 4;17(1):6.
doi: 10.1186/s12976-020-00124-9.

Modeling and dynamic analysis of tuberculosis in mainland China from 1998 to 2017: the effect of DOTS strategy and further control

Siyu Liu  1 , Yingjie Bi  2 , Yawen Liu  3
Affiliations

Modeling and dynamic analysis of tuberculosis in mainland China from 1998 to 2017: the effect of DOTS strategy and further control

Siyu Liu et al. Theor Biol Med Model. .

Abstract

Background: Tuberculosis (TB) is one of the most important health topics in the world. Directly observed treatment and short course chemotherapy (DOTS) strategy combines medicine care and modern health system firmly, and it has been carried out by World Health Organization (WHO) since 1997. In the struggle with TB, China has promoted the process of controlling the disease actively, and the full coverage of DOTS strategy has been reached around 2004. Mathematical modeling is a very useful tool to study the transmission of diseases. Understanding the impact of DOTS strategy on the control of TB is important for designing further prevention strategy.

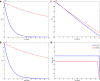
Methods: We investigate the impact of control strategy on the transmission of TB in China by dynamic model. Then we discuss further control for TB aiming at developing new vaccine and improving treatment. The optimal control problem, minimizing the total number of infectious individuals with the lowest cost, is proposed and analyzed by Pontryagin's maximum principle. Numerical simulations are provided to illustrate the theoretical results.

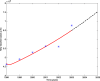
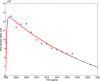
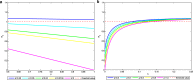
Results: Theoretical analysis for the epidemic model is given. Based on the data reported by National Bureau of Statistics of China (NBSC), the basic reproduction number of each stage is estimated and compared, and they are [Formula: see text] and [Formula: see text], respectively. Optimal control strategy for further control is designed and proved well. An intuitionistic comparison between the optimal control strategy and the current control strategy is given.

Conclusions: The diagnosis and treatment of TB in China have been promoted a lot and the [Formula: see text] is reduced by the full coverage of DOTS strategy. However, the [Formula: see text] in China is still greater than 1 now. The relationship between [Formula: see text] and vaccination strategy is shown. Optimal strategy aiming at exposed and infected population is suggested for further control.

Keywords: DOTS strategy; Epidemic model; Optimal control; Tuberculosis.

PubMed Disclaimer

Conflict of interest statement

The authors declare that they have no competing interests.

Figures

Fig. 1
Fig. 1
Goodness of fit for the first stage of TB trends
Fig. 2
Fig. 2
Goodness of fit for the second stage of TB trends
Fig. 3
Fig. 3
a The effect of p on R0 when k is varied. b The effect of k on R0 when p is varied
Fig. 4
Fig. 4
Comparison between the current TB control strategy and optimal control strategy
See this image and copyright information in PMC

References

    1. World Health Report 2001: Global Tuberculosis Control. http://apps.who.int/iris/bitstream/10665/63835/4/WHO_CDS_TB_2001.287.pdf.
    1. Global Tuberculosis Report 2018. https://apps.who.int/iris/bitstream/handle/10665/274453/9789241565646-en....
    1. Xu B, Hu Y, Zhao Q, Wang W, Jiang W, Zhao G. Molecular epidemiology of tb - its impact on multidrug-resistant tuberculosis control in china. Int J Mycobact. 2015;4:134. doi: 10.1016/j.ijmyco.2014.09.003. - DOI
    1. Pinto E, Nepomuceno E, Campanharo A. Influence of contact network topology on the spread of tuberculosis, vol. 1068: Springer; 2019, pp. 81–88. 10.1007/978-3-030-36636-0_6.
    1. Aparicio J, Castillo-Chavez C. Mathematical modelling of tuberculosis epidemics. Math Biosci Eng. 2009;6:209–237. doi: 10.3934/mbe.2009.6.209. - DOI - PubMed

Publication types