Deforestation and world population sustainability: a quantitative analysis
- PMID: 32376879
- PMCID: PMC7203172
- DOI: 10.1038/s41598-020-63657-6
Deforestation and world population sustainability: a quantitative analysis
Abstract
In this paper we afford a quantitative analysis of the sustainability of current world population growth in relation to the parallel deforestation process adopting a statistical point of view. We consider a simplified model based on a stochastic growth process driven by a continuous time random walk, which depicts the technological evolution of human kind, in conjunction with a deterministic generalised logistic model for humans-forest interaction and we evaluate the probability of avoiding the self-destruction of our civilisation. Based on the current resource consumption rates and best estimate of technological rate growth our study shows that we have very low probability, less than 10% in most optimistic estimate, to survive without facing a catastrophic collapse.
Conflict of interest statement
The authors declare no competing interests.
Figures


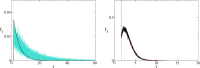
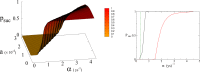



References
-
- Waring, R. H. & Running, S. W. Forest Ecosystems: Analysis at Multiple Scales (Academic Press, 2007).
-
- The State of the World’s Forests 2018. Forest Pathways to Sustainable Development, Food and Agriculture Organization of the United Nations Rome (2018).
-
- Bologna M, Flores JC. A simple mathematical model of society collapse applied to Easter Island. EPL. 2008;81:48006. doi: 10.1209/0295-5075/81/48006. - DOI
-
- U.S. Energy Information Administration (EIA), https://www.eia.gov/international/data/world.
LinkOut - more resources
Full Text Sources

