On a comprehensive model of the novel coronavirus (COVID-19) under Mittag-Leffler derivative
- PMID: 32390692
- PMCID: PMC7205740
- DOI: 10.1016/j.chaos.2020.109867
On a comprehensive model of the novel coronavirus (COVID-19) under Mittag-Leffler derivative
Abstract
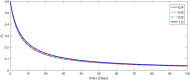
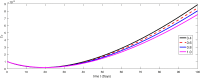
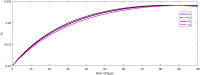
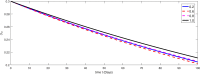
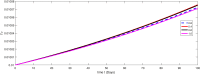
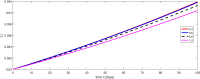
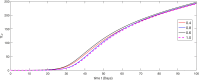
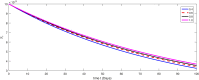
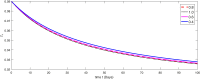
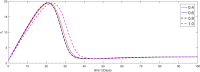
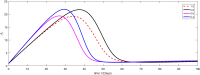
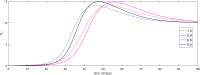
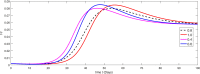
The major purpose of the presented study is to analyze and find the solution for the model of nonlinear fractional differential equations (FDEs) describing the deadly and most parlous virus so-called coronavirus (COVID-19). The mathematical model depending of fourteen nonlinear FDEs is presented and the corresponding numerical results are studied by applying the fractional Adams Bashforth (AB) method. Moreover, a recently introduced fractional nonlocal operator known as Atangana-Baleanu (AB) is applied in order to realize more effectively. For the current results, the fixed point theorems of Krasnoselskii and Banach are hired to present the existence, uniqueness as well as stability of the model. For numerical simulations, the behavior of the approximate solution is presented in terms of graphs through various fractional orders. Finally, a brief discussion on conclusion about the simulation is given to describe how the transmission dynamics of infection take place in society.
Keywords: 26A33; 34A08; 35R11; Adams Bashforth method; Attangana-Baleanu derivative; COVID-19; Existence and stability theory; Fixed point theorem.
© 2020 Elsevier Ltd. All rights reserved.
Conflict of interest statement
We declare that none of the author has the competing or conflict of interest.
Figures

References
-
- Tyrrell D.A., Bynoe M.L. Cultivation of viruses from a high proportion of patients with colds. Lancet. 1966;1:76–77. - PubMed
-
- Kahn J.S., McIntosh K. History and recent advances in coronavirus discovery. Pediatric Infect Dis J. 2005;24(11):223–227. - PubMed
-
- Kilbas A.A., Shrivastava H.M., Trujillo J.J. Elsevier; Amsterdam: 2006. Theory and applications of fractional differential equations.
LinkOut - more resources
Full Text Sources

