On a comprehensive model of the novel coronavirus (COVID-19) under Mittag-Leffler derivative

Abstract

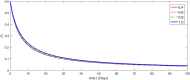
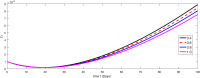
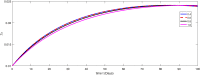
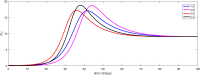
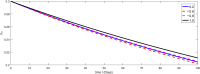
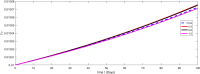
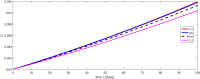
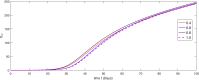
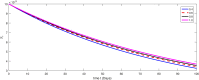
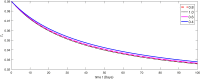
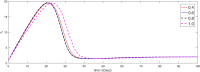
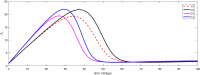
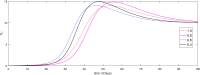
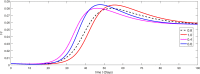
The major purpose of the presented study is to analyze and find the solution for the model of nonlinear fractional differential equations (FDEs) describing the deadly and most parlous virus so-called coronavirus (COVID-19). The mathematical model depending of fourteen nonlinear FDEs is presented and the corresponding numerical results are studied by applying the fractional Adams Bashforth (AB) method. Moreover, a recently introduced fractional nonlocal operator known as Atangana-Baleanu (AB) is applied in order to realize more effectively. For the current results, the fixed point theorems of Krasnoselskii and Banach are hired to present the existence, uniqueness as well as stability of the model. For numerical simulations, the behavior of the approximate solution is presented in terms of graphs through various fractional orders. Finally, a brief discussion on conclusion about the simulation is given to describe how the transmission dynamics of infection take place in society.

Keywords: 26A33; 34A08; 35R11; Adams Bashforth method; Attangana-Baleanu derivative; COVID-19; Existence and stability theory; Fixed point theorem.

Fig. 1

Graphical representation of numerical solution for susceptible class of bats at various fractional of the considered model (1).

Fig. 2

Graphical representation of numerical solution for exposed bats at various fractional of the considered model (1).

Fig. 3

Graphical representation of numerical solution for infected bats at various fractional of the considered model (1).

Fig. 4

Graphical representation of numerical solution for removed class of bats at various fractional of the considered model (1).

Fig. 5

Graphical representation of numerical solution for susceptible host at various fractional of the considered model (1).

Fig. 6

Graphical representation of numerical solution for exposed hosts at various fractional of the considered model (1).

Fig. 7

Graphical representation of numerical solution for infected host at various fractional of the considered model (1).

Fig. 8

Graphical representation of numerical solution for removed host at various fractional of the considered model (1).

Fig. 9

Graphical representation of numerical solution for susceptible people at various fractional of the considered model (1).

Fig. 10

Graphical representation of numerical solution for exposed people at various fractional of the considered model (1).

Fig. 11

Graphical representation of numerical solution for symptomatic infected people at various fractional of the considered model (1).

Fig. 12

Graphical representation of numerical solution for asymptomatic infected people at various fractional of the considered model (1).

Fig. 13

Graphical representation of numerical solution for population of removed people due to death or recovered various fractional of the considered model (1).

Fig. 14

Graphical representation of numerical solution for population of virus in reservoir various fractional of the considered model (1).