Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2020 Jul:136:109889.
doi: 10.1016/j.chaos.2020.109889. Epub 2020 May 13.

A model based study on the dynamics of COVID-19: Prediction and control

Manotosh Mandal  1   2 , Soovoojeet Jana  3 , Swapan Kumar Nandi  4 , Anupam Khatua  2 , Sayani Adak  3 , T K Kar  2
Affiliations

A model based study on the dynamics of COVID-19: Prediction and control

Manotosh Mandal et al. Chaos Solitons Fractals. 2020 Jul.

Abstract

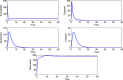
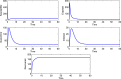
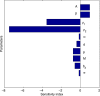
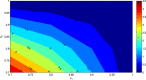
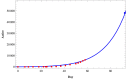
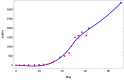
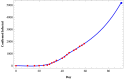
As there is no vaccination and proper medicine for treatment, the recent pandemic caused by COVID-19 has drawn attention to the strategies of quarantine and other governmental measures, like lockdown, media coverage on social isolation, and improvement of public hygiene, etc to control the disease. The mathematical model can help when these intervention measures are the best strategies for disease control as well as how they might affect the disease dynamics. Motivated by this, in this article, we have formulated a mathematical model introducing a quarantine class and governmental intervention measures to mitigate disease transmission. We study a thorough dynamical behavior of the model in terms of the basic reproduction number. Further, we perform the sensitivity analysis of the essential reproduction number and found that reducing the contact of exposed and susceptible humans is the most critical factor in achieving disease control. To lessen the infected individuals as well as to minimize the cost of implementing government control measures, we formulate an optimal control problem, and optimal control is determined. Finally, we forecast a short-term trend of COVID-19 for the three highly affected states, Maharashtra, Delhi, and Tamil Nadu, in India, and it suggests that the first two states need further monitoring of control measures to reduce the contact of exposed and susceptible humans.

Keywords: Bang-bang and singular control; Basic reproduction number; Short term prediction of COVID-19; Theoretical epidemiology; Transcritical bifurcation.

PubMed Disclaimer

Conflict of interest statement

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Figures

Fig. 1
Fig. 1
Flow diagram of disease transmission.
Fig. 2
Fig. 2
Dynamical behavior around DFE.
Fig. 3
Fig. 3
Dynamical behavior around EE.
Fig. 4
Fig. 4
The transcritical bifurcation diagram depicts the exchange of stability at R0=1.
Fig. 5
Fig. 5
Sensitivity index of R0 against some parameters.
Fig. 6
Fig. 6
Contour plot of R0 as a function of β and ρ1.
Fig. 7
Fig. 7
Contour plot of R0 as a function of ρ1 and ρ2.
Fig. 8
Fig. 8
Variation of population in presence and absence of control strategy.
Fig. 9
Fig. 9
Variation of the adjoint variables when control applied optimally.
Fig. 10
Fig. 10
Variation of the control strategy of control parameter M.
Fig. 11
Fig. 11
Active COVID-19 cases in Maharashtra.
Fig. 12
Fig. 12
Active COVID-19 cases in Delhi
Fig. 13
Fig. 13
Active COVID-19 cases in Tamil Nadu.
Fig. 14
Fig. 14
Confirmed COVID-19 cases in Maharashtra.
Fig. 15
Fig. 15
Confirmed COVID-19 cases in Delhi.
Fig. 16
Fig. 16
Confirmed COVID-19 cases in Tamil Nadu.
See this image and copyright information in PMC

Similar articles

See all similar articles

Cited by

See all "Cited by" articles

References

    1. Bernoulli D. Mem Math Phy Acad Roy Sci Paris. 1760. Essai dune nouvelle analyse de la mortalite causee par la petite verole; p. 145.
    1. Birkoff G., Rota G.C. Ginn; Boston: 1982. Ordinary differential equations.
    1. Buonomo B., dOnofrio A., Lacitignola D. Global stability of an SIR epidemic model with information dependent vaccination. Math Biosci. 2008;216:9–16. - PubMed
    1. Chakraborty T., Ghosh I. Real-time forecasts and risk assessment of novel coronavirus (COVID-19) cases: a data-driven analysis. Chaos Solitons Fractals. 2020 doi: 10.1016/j.chaos.2020.109850. - DOI - PMC - PubMed
    1. Diekmann O., JAJ M., JAP H. On the definition on the computation of the basic reproduction number ratio r0 in models for infectious diseases in heterogeneous population. J Math Biol. 1990;28:365–382. - PubMed