Combining Multiple Functional Connectivity Methods to Improve Causal Inferences
- PMID: 32427070
- PMCID: PMC8132338
- DOI: 10.1162/jocn_a_01580
Combining Multiple Functional Connectivity Methods to Improve Causal Inferences
Abstract
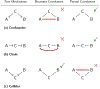
Cognition and behavior emerge from brain network interactions, suggesting that causal interactions should be central to the study of brain function. Yet, approaches that characterize relationships among neural time series-functional connectivity (FC) methods-are dominated by methods that assess bivariate statistical associations rather than causal interactions. Such bivariate approaches result in substantial false positives because they do not account for confounders (common causes) among neural populations. A major reason for the dominance of methods such as bivariate Pearson correlation (with functional MRI) and coherence (with electrophysiological methods) may be their simplicity. Thus, we sought to identify an FC method that was both simple and improved causal inferences relative to the most popular methods. We started with partial correlation, showing with neural network simulations that this substantially improves causal inferences relative to bivariate correlation. However, the presence of colliders (common effects) in a network resulted in false positives with partial correlation, although this was not a problem for bivariate correlations. This led us to propose a new combined FC method (combinedFC) that incorporates simple bivariate and partial correlation FC measures to make more valid causal inferences than either alone. We release a toolbox for implementing this new combinedFC method to facilitate improvement of FC-based causal inferences. CombinedFC is a general method for FC and can be applied equally to resting-state and task-based paradigms.
Figures


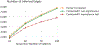


References
-
- Barbas H (2015). General Cortical and Special Prefrontal Connections: Principles from Structure to Function. Annual Review of Neuroscience, 38(1), 269–289. - PubMed
-
- Bishop CM (2006). Pattern recognition and machine learning. Springer.
-
- Bühlmann P, & Van De Geer S (2011). Statistics for high-dimensional data: Methods, theory and applications. Springer Science & Business Media.
-
- Chickering DM (2002). Optimal structure identification with greedy search. Journal of Machine Learning Research, 3(Nov), 507–554.
-
- Ciric R, Wolf DH, Power JD, Roalf DR, Baum GL, Ruparel K, Shinohara RT, Elliott MA, Eickhoff SB, Davatzikos C, Gur RC, Gur RE, Bassett DS, & Satterthwaite TD (2017). Benchmarking of participant-level confound regression strategies for the control of motion artifact in studies of functional connectivity. NeuroImage, 154, 174–187. - PMC - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical

