Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2020 Dec;75(12):1643-1647.
doi: 10.1111/anae.15151. Epub 2020 Jun 19.

Managing the R0 of COVID-19: mathematics fights back

J J Pandit  1
Affiliations

Managing the R0 of COVID-19: mathematics fights back

J J Pandit. Anaesthesia. 2020 Dec.
No abstract available

PubMed Disclaimer

Figures

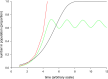
Figure 1
Figure 1
Three models of population (viral) growth: exponential (Eqn 1; red), logistic (Eqn 2, black) and logistic map (Eqn 3, green). Different values have been used to separate the lines. Note that whereas in exponential, R0 value is constant, it varies for the other two models depending on the time‐point it is measured
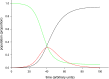
Figure 2
Figure 2
Example of an SIR model plot for a hypothetical infectious disease. The green curve is the susceptible population; the red curve is the infected, and the black curve is the recovered. Note the inverse relationship between the susceptible and recovered, with the infected being the balance
Figure 3
Figure 3
Estimate of the proportion of population needed to be immune to achieve herd immunity, as a function of R0. Note that for R0 < 2, the relationship is very steep with < 50% of population needing immunity,
See this image and copyright information in PMC

Comment in

  • Measuring R0.
    Gwinnutt C. Gwinnutt C. Anaesthesia. 2021 Mar;76 Suppl 3:26. doi: 10.1111/anae.15351. Epub 2020 Dec 23. Anaesthesia. 2021. PMID: 33253474 No abstract available.

References

    1. Box GEP. Science and statistics. Journal of the American Statistical Association 1976; 71: 791–9.
    1. May RM, Anderson B. Infectious Diseases of Humans: Dynamics and Control. Oxford: Oxford University Press, 1992.
    1. Cramer JS. The early origins of the logit model. Studies in History and Philosophy of Science 2004; 35: 613–26.
    1. May RM. Simple mathematical models with very complicated dynamics. Nature 1976; 261: 459–67. - PubMed
    1. Alimohamadi Y, Taghdir M, Sepandi M. The estimate of the basic reproduction number for novel coronavirus disease (COVID‐19): a systematic review and meta‐analysis. Journal of Preventive Medicine and Public Health 2020; 53: 151–7. - PMC - PubMed