Insights into variation in meiosis from 31,228 human sperm genomes
- PMID: 32494014
- PMCID: PMC7351608
- DOI: 10.1038/s41586-020-2347-0
Insights into variation in meiosis from 31,228 human sperm genomes
Abstract
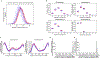
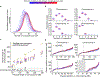
Meiosis, although essential for reproduction, is also variable and error-prone: rates of chromosome crossover vary among gametes, between the sexes, and among humans of the same sex, and chromosome missegregation leads to abnormal chromosome numbers (aneuploidy)1-8. To study diverse meiotic outcomes and how they covary across chromosomes, gametes and humans, we developed Sperm-seq, a way of simultaneously analysing the genomes of thousands of individual sperm. Here we analyse the genomes of 31,228 human gametes from 20 sperm donors, identifying 813,122 crossovers and 787 aneuploid chromosomes. Sperm donors had aneuploidy rates ranging from 0.01 to 0.05 aneuploidies per gamete; crossovers partially protected chromosomes from nondisjunction at the meiosis I cell division. Some chromosomes and donors underwent more-frequent nondisjunction during meiosis I, and others showed more meiosis II segregation failures. Sperm genomes also manifested many genomic anomalies that could not be explained by simple nondisjunction. Diverse recombination phenotypes-from crossover rates to crossover location and separation, a measure of crossover interference-covaried strongly across individuals and cells. Our results can be incorporated with earlier observations into a unified model in which a core mechanism, the variable physical compaction of meiotic chromosomes, generates interindividual and cell-to-cell variation in diverse meiotic phenotypes.
Conflict of interest statement
Competing Interests
A.D.B. and S.A.M. are inventors on a United States Provisional Patent application (PCT/US2019/029427; applicant: President and Fellows of Harvard College) currently in PCT stage relating to droplet-based genomic DNA capture, amplification and sequencing that is capable of obtaining high-throughput single-cell sequence from individual mammalian cells, including sperm cells. A.D.B. is an occasional consultant for Ohana Biosciences since October 2019. The other authors declare no competing interests.
Figures
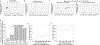








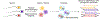


Comment in
-
Sequencing sperm to untangle meiotic variation.Nat Rev Genet. 2020 Aug;21(8):447. doi: 10.1038/s41576-020-0259-3. Nat Rev Genet. 2020. PMID: 32561863 No abstract available.
-
Limitations of gamete sequencing for crossover analysis.Nature. 2022 Jun;606(7913):E1-E3. doi: 10.1038/s41586-022-04693-2. Epub 2022 Jun 8. Nature. 2022. PMID: 35676433 Free PMC article. No abstract available.
References
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

