On the Interpretability of Artificial Intelligence in Radiology: Challenges and Opportunities
- PMID: 32510054
- PMCID: PMC7259808
- DOI: 10.1148/ryai.2020190043
On the Interpretability of Artificial Intelligence in Radiology: Challenges and Opportunities
Abstract
As artificial intelligence (AI) systems begin to make their way into clinical radiology practice, it is crucial to assure that they function correctly and that they gain the trust of experts. Toward this goal, approaches to make AI "interpretable" have gained attention to enhance the understanding of a machine learning algorithm, despite its complexity. This article aims to provide insights into the current state of the art of interpretability methods for radiology AI. This review discusses radiologists' opinions on the topic and suggests trends and challenges that need to be addressed to effectively streamline interpretability methods in clinical practice. Supplemental material is available for this article. © RSNA, 2020 See also the commentary by Gastounioti and Kontos in this issue.
2020 by the Radiological Society of North America, Inc.
Conflict of interest statement
Figures
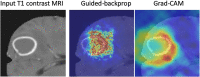

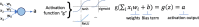

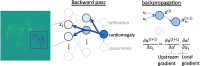

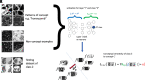

References
-
- Topol EJ. High-performance medicine: the convergence of human and artificial intelligence. Nat Med 2019;25(1):44–56. - PubMed
-
- Szegedy C, Zaremba W, Sutskever I, et al. . Intriguing properties of neural networks. ArXiv 13126199 [preprint] http://adsabs.harvard.edu/abs/2013arXiv1312.6199S. Posted December 2013. Accessed January 6, 2020.
-
- Lipton ZC. The mythos of model interpretability. ArXiv 1606.03490v3 [preprint] http://arxiv.org/abs/1606.03490. Posted June 10, 2016. Accessed January 6, 2020.
-
- Van Lent M, Fisher W, Mancuso M. An explainable artificial intelligence system for small-unit tactical behavior. In: Proceedings of the Nineteenth National Conference on Artificial Intelligence. San Jose, Calif, July 25–29, 2004. Palo Alto, Calif: Association for the Advancement of Artificial Intelligence, 2004; 900–907.
-
- Gunning D. Explainable artificial intelligence (XAI). Defense Advanced Research Projects Agency (DARPA) Web site. https://www.darpa.mil/attachments/XAIProgramUpdate.pdf. Updated November 2017. Accessed January 6, 2020.
Publication types
Grants and funding
LinkOut - more resources
Full Text Sources
Research Materials

