Awareness-driven Behavior Changes Can Shift the Shape of Epidemics Away from Peaks and Towards Plateaus, Shoulders, and Oscillations

Abstract

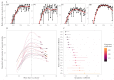
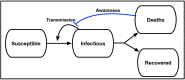
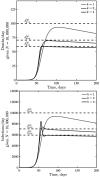
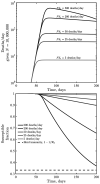
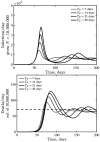
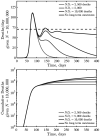
The COVID-19 pandemic has caused more than 1,000,000 reported deaths globally, of which more than 200,000 have been reported in the United States as of October 1, 2020. Public health interventions have had significant impacts in reducing transmission and in averting even more deaths. Nonetheless, in many jurisdictions the decline of cases and fatalities after apparent epidemic peaks has not been rapid. Instead, the asymmetric decline in cases appears, in most cases, to be consistent with plateau-or shoulder-like phenomena - a qualitative observation reinforced by a symmetry analysis of US state-level fatality data. Here we explore a model of fatality-driven awareness in which individual protective measures increase with death rates. In this model, fast increases to the peak are often followed by plateaus, shoulders, and lag-driven oscillations. The asymmetric shape of model-predicted incidence and fatality curves are consistent with observations from many jurisdictions. Yet, in contrast to model predictions, we find that population-level mobility metrics usually increased from low early-outbreak levels before peak levels of fatalities. We show that incorporating fatigue and long-term behavior change can reconcile the apparent premature relaxation of mobility reductions and help understand when post-peak dynamics are likely to lead to a resurgence of cases.

FIG. 1:

Plateaus and shoulder-like dynamics in COVID-19 fatalities. (A) Examples of daily number of reported deaths for COVID-19 (black points and lines) and the corresponding locally estimated scatterplot smoothing (LOESS) curves (red lines) in four states, including two estimated to be the most plateau-like (Minnesota and North Carolina) and two estimated to be the most peak-like (Indiana and Maryland). Daily number of deaths is smoothed in log space, only including days with one or more reported deaths. We restrict our analysis to states in which the peak smoothed death is greater than 10 as of June 7, 2020 (resulting in 17 states in total). (B) Smoothed daily number of reported deaths centered around the first peak time t_P across 17 states. Smoothed death curves are plotted between t_P − Δt and t_P + Δt, where Δt is defined such that smoothed death at time t_P − Δt corresponds to 10% of the smoothed peak value. (C) Measured symmetry coefficient and confidence intervals. Symmetry coefficient is calculated by dividing the death value at time t_P − Δt by the death value at time t_P + Δt. If the death curve is symmetric, the symmetry coefficient should equal 1. Confidence intervals are calculated by bootstrapping across the date of deaths for each individual 1000 times and recalculating the symmetry coefficient (after smoothing each bootstrap time series). LOESS smoothing is performed by using the loess function in R.

FIG. 2:

Schematic of an SEIR model with awareness-driven social distancing. Transmission is reduced based on short- and/or long-term awareness of population-level disease severity (i.e., fatalities).

FIG. 3:

Infections and deaths per day in a death-awareness based social distancing model. Simulations have the epidemiological parameters β = 0.5 /day, μ = 1/2 /day, γ = 1/6/day, and f_D = 0.01, with variation in k = 1, 2 and 4. We assume Nδ_c = 50 /day in all cases.

FIG. 4:

Dynamics given variation in the critical fatality awareness level, δ_c for awareness k = 2. Panels show deaths/day (top) and the susceptible fraction as a function of time (bottom), the latter compared to a herd immunity level when only a fraction $1/{\mathcal{R}}_0$ remain susceptible. These simulations share the epidemiological parameters β = 0.5 /day, μ = 1/2 /day, γ = 1/6 /day, and f_D = 0.01.

FIG. 5:

Emergence of oscillatory dynamics in a death-driven awareness model of social distancing given lags between infection and fatality. Awareness is k = 2 and all other parameters as in Figure 3. The dashed lines for fatalities expected quasi-stationary value δ^(q).

FIG. 6:

SEIR dynamics with short- and long-term awareness. Model parameters are β = 0.5 /day, μ = 1/2 /day, γ = 1/6 /day, T_H = 14 days, f_D = 0.01, N = 10⁷, k = 2, Nδ_c = 50 /day (short-term awareness), with varying ND_c (long-term awareness) as shown in the legend. The dashed line (top) denotes δ^(q) due to short-term distancing alone.

FIG. 7:

Phase-plane visualizations of deaths vs. mobility for state-level data (top) and SEIR models (bottom panels). (Top) Deaths and mobility indexes through time for the 17 analyzed states. Both data series are smoothed. Time windows as in 1. (B) Dynamics of effective behavior and death rates in a SEIR model with short- and long-term awareness. Curves denote different assumptions regarding long-term awareness, in each case β = 0.5/day, μ = 0.5/day, γ = 1/6/day, such that ${\mathcal{R}}_0=3$, with k = 2, γ_H = 1/21/day, and f_D = 0.01. The short-term awareness corresponds go Nδ_c = 50 deaths/day. Thin lines denote full dynamics over 400 days; thick lines denote the dynamics near the case fatality peak. (C) Dynamics of effective behavior and death rates in a SEIR model with awareness and fatigue. The three different curves denote different assumptions regarding long-term awareness, in each case β = 0.5/day, μ = 0.5/day, γ = 1/6/day, such that ${\mathcal{R}}_0=3$, with k = 2, γ_H = 1/21/day, f_D = 0.01, and ∈ = 1/7/day. The short-term awareness corresponds go Nδ_c = 50 deaths/day. The force of infection does not include long term changes in behavior beyond mobility, i.e., g(D) = 1. (D) As in (C), but the force of infection includes long-term changes in behavior, i.e., g(D) = 1/(1+(D/Dc)^k).