Theoretical issues in deep networks

Abstract

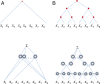
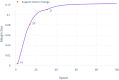
While deep learning is successful in a number of applications, it is not yet well understood theoretically. A theoretical characterization of deep learning should answer questions about their approximation power, the dynamics of optimization, and good out-of-sample performance, despite overparameterization and the absence of explicit regularization. We review our recent results toward this goal. In approximation theory both shallow and deep networks are known to approximate any continuous functions at an exponential cost. However, we proved that for certain types of compositional functions, deep networks of the convolutional type (even without weight sharing) can avoid the curse of dimensionality. In characterizing minimization of the empirical exponential loss we consider the gradient flow of the weight directions rather than the weights themselves, since the relevant function underlying classification corresponds to normalized networks. The dynamics of normalized weights turn out to be equivalent to those of the constrained problem of minimizing the loss subject to a unit norm constraint. In particular, the dynamics of typical gradient descent have the same critical points as the constrained problem. Thus there is implicit regularization in training deep networks under exponential-type loss functions during gradient flow. As a consequence, the critical points correspond to minimum norm infima of the loss. This result is especially relevant because it has been recently shown that, for overparameterized models, selection of a minimum norm solution optimizes cross-validation leave-one-out stability and thereby the expected error. Thus our results imply that gradient descent in deep networks minimize the expected error.

Keywords: approximation; deep learning; generalization; machine learning; optimization.

Fig. 1.

Top graphs are associated to functions. Each Bottom diagram (Insets) depicts the ideal network approximating the function above. (Inset A) A shallow universal network in 8 variables and $N$ units approximates a generic function of 8 variables $f\left(x_1,\dots ,x_8\right)$. (Inset B) A hierarchical network at the bottom in $n=8$ variables, which approximates well functions of the form $f\left(x_1,\dots ,x_8\right)=h_3\left(h_{21}\left(h_{11}\left(x_1,x_2\right),h_{12}\left(x_3,x_4\right)\right),h_{22}\left(h_{13}\left(x_5,x_6\right),h_{14}\left(x_7,x_8\right)\right)\right)$ as represented by the binary graph above. In the approximating network each of the $n-1$ nodes in the graph of the function corresponds to a set of ReLU units. Similar to the shallow network, a hierarchical network is universal; that is, it can approximate any continuous function; the text discusses how it can approximate a subclass of compositional functions exponentially better than a shallow network. Redrawn from ref. .

Fig. 2.

Empirical evidence of a small generalization gap by normalized networks with respect to the cross-entropy loss. Left graph shows testing vs. training cross-entropy loss for networks each trained on the same datasets (CIFAR-10) (46) but with different initializations, yielding zero classification error on the training set but different testing errors. Right graph shows the same data, that is, testing vs. training loss for the same networks, now normalized by dividing each weight by the Frobenius norm of its layer. Note that all points have zero classification error at training. The red circle on the top right refers to a network trained on the same CIFAR-10 dataset but with randomized labels. It shows zero classification error at training and test error at chance level. The top line is a square-loss regression of slope 1 with positive intercept. The bottom line is the diagonal at which training and test loss are equal. The networks are three-layer convolutional networks. Left graph can be considered as a visualization of generalization bounds when the Rademacher complexity is not controlled. Right graph is a visualization of the same relation for normalized networks that is $L\left(\rho f\left(V;x\right)\right)\le \widehat{L}\left(\rho f\left(V;x\right)\right)+c_1\rho {\mathbb{R}}_N\left(\stackrel{\sim }{\mathbb{F}}\right)+c_2\sqrt{\ln \left(\frac{1}{\delta }\right)/2N}$ for $\rho =1$. Under our conditions for $N$ and for the architecture of the network the terms $c_1{\mathbb{R}}_N\left(\stackrel{\sim }{\mathbb{F}}\right)+c_2\sqrt{\ln \left(\frac{1}{\delta }\right)/2N}$ represent a small offset. Note that the exponential loss is not a better proxy for the classification loss for large $\rho$. Empirically for these datasets, the test exponential loss with $\rho =1$ provides a ranking that approximately agrees with the test classification ranking. From ref. .

Fig. 3.

Monotonic increase of the margin: the growth of the margin ${\text{min}}_n{y}_{n}f\left(V;x_n\right)$ in the binary case. The network converges to 100% training accuracy in epoch 3 and changes the support vectors three times (red circles—the numbers above them correspond to the index of the datapoint that becomes the support vector) before stabilizing. As predicted by theory, the margin is nondecreasing. As the support vectors change, note that the rate of margin growth accelerates.