Novel Corona virus disease infection in Tunisia: Mathematical model and the impact of the quarantine strategy

Abstract

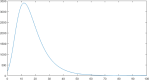
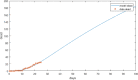
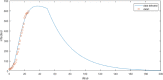
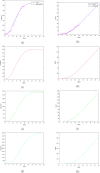
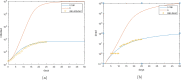
Corona virus disease (COVID-19) is an extremely serious infection with an extremely high death rate worldwide. In March, the disease was declared a "global pandemic" by the World Health Organization (WHO). Until now, there is no known vaccine or drug, since the unknown things related to the disease are more important than our theoretical and empirical knowledge. However, mathematical modeling and the estimation of the basic number of reproductions can provide clarifications in order to determine the potential and severity of this epidemic and therefore provide essential information to identify the type of measures and interventions to be taken to control the intensity of the spread of the disease. Hence, in this paper, we propose a new deterministic compartmental model based on the clinical progression of the disease, the epidemiological state of the individuals and the intervention for the dynamics of COVID-19 infections. Our approach consists of seven phenotypes: the susceptible humans, exposed humans, infectious humans, the recovered humans, the quarantine population, there recovered-exposed and deceased population. We proved first through mathematical approach the positivity, boundness and existence of a solution to the considered model. We also studied the existence of the disease free equilibrium and corresponding stability. Our work shows, in particular, that the disease will decrease if the number of reproduction R ₀ was less than one. Moreover, the impact of the quarantine strategies to reduce the spread of this disease is discussed. The theoretical results are validated by some numerical simulations of the system of the epidemic's differential equations. It should be mentioned that, the error between the considered model and the official data curve is quite small.

Keywords: 34A34; 34C60; 92Bxx; 93A30; Mathematical modelling; Nonlinear differential systems; Qualitative study; Simulation.

Fig. 2.1

Model flow chart showing the compartments.

Fig. 4.1

Infected population.

Fig. 4.2

Exposed population.

Fig. 4.3

dead population.

Fig. 4.4

Infected population.

Fig. 4.5

Recovered population.

Fig. 4.6

Dead population.

Fig. 4.7

a-b) Infected population and Dead population with ${\lambda }_3=0.166$ which was our case, c-d) Infected population and Dead population with ${\lambda }_3=0.15,$ e-f) Infected population and Dead population with ${\lambda }_3=0.13,$ g-h) Infected population and Dead population with ${\lambda }_3=0.1$.

Fig. 4.8

a) Infected population and b) Dead population with different ${\lambda }_3=0.166,0.15,0.13,0.1$.

Fig. 4.9

a) Infected population and b) Dead population with different ${\lambda }_3=0.166,0$.