Graphical calibration curves and the integrated calibration index (ICI) for survival models
- PMID: 32548928
- PMCID: PMC7497089
- DOI: 10.1002/sim.8570
Graphical calibration curves and the integrated calibration index (ICI) for survival models
Abstract
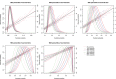
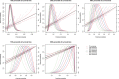
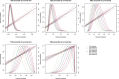
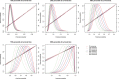
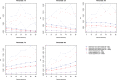
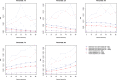
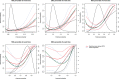
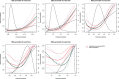
In the context of survival analysis, calibration refers to the agreement between predicted probabilities and observed event rates or frequencies of the outcome within a given duration of time. We aimed to describe and evaluate methods for graphically assessing the calibration of survival models. We focus on hazard regression models and restricted cubic splines in conjunction with a Cox proportional hazards model. We also describe modifications of the Integrated Calibration Index, of E50 and of E90. In this context, this is the average (respectively, median or 90th percentile) absolute difference between predicted survival probabilities and smoothed survival frequencies. We conducted a series of Monte Carlo simulations to evaluate the performance of these calibration measures when the underlying model has been correctly specified and under different types of model mis-specification. We illustrate the utility of calibration curves and the three calibration metrics by using them to compare the calibration of a Cox proportional hazards regression model with that of a random survival forest for predicting mortality in patients hospitalized with heart failure. Under a correctly specified regression model, differences between the two methods for constructing calibration curves were minimal, although the performance of the method based on restricted cubic splines tended to be slightly better. In contrast, under a mis-specified model, the smoothed calibration curved constructed using hazard regression tended to be closer to the true calibration curve. The use of calibration curves and of these numeric calibration metrics permits for a comprehensive comparison of the calibration of competing survival models.
Keywords: calibration; model validation; random forests; survival analysis; time-to-event model.
© 2020 The Authors. Statistics in Medicine published by John Wiley & Sons, Ltd.
Figures





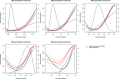
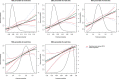
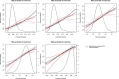
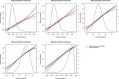
Similar articles
-
Graphical calibration curves and the integrated calibration index (ICI) for competing risk models.Diagn Progn Res. 2022 Jan 17;6(1):2. doi: 10.1186/s41512-021-00114-6. Diagn Progn Res. 2022. PMID: 35039069 Free PMC article.
-
The Integrated Calibration Index (ICI) and related metrics for quantifying the calibration of logistic regression models.Stat Med. 2019 Sep 20;38(21):4051-4065. doi: 10.1002/sim.8281. Epub 2019 Jul 3. Stat Med. 2019. PMID: 31270850 Free PMC article.
-
The Impact of Violation of the Proportional Hazards Assumption on the Calibration of the Cox Proportional Hazards Model.Stat Med. 2025 Jun;44(13-14):e70161. doi: 10.1002/sim.70161. Stat Med. 2025. PMID: 40492822 Free PMC article.
-
Performance metrics for models designed to predict treatment effect.BMC Med Res Methodol. 2023 Jul 8;23(1):165. doi: 10.1186/s12874-023-01974-w. BMC Med Res Methodol. 2023. PMID: 37422647 Free PMC article.
-
Using Joint Longitudinal and Time-to-Event Models to Improve the Parameterization of Chronic Disease Microsimulation Models: an Application to Cardiovascular Disease.medRxiv [Preprint]. 2024 Oct 29:2024.10.27.24316240. doi: 10.1101/2024.10.27.24316240. medRxiv. 2024. PMID: 39574877 Free PMC article. Preprint.
Cited by
-
Investigation of end-stage kidney disease risk prediction in an ethnically diverse cohort of people with type 2 diabetes: use of kidney failure risk equation.BMJ Open Diabetes Res Care. 2024 Sep 13;12(4):e004282. doi: 10.1136/bmjdrc-2024-004282. BMJ Open Diabetes Res Care. 2024. PMID: 39277182 Free PMC article.
-
ECG-Based Deep Learning and Clinical Risk Factors to Predict Atrial Fibrillation.Circulation. 2022 Jan 11;145(2):122-133. doi: 10.1161/CIRCULATIONAHA.121.057480. Epub 2021 Nov 8. Circulation. 2022. PMID: 34743566 Free PMC article.
-
Cohort design and natural language processing to reduce bias in electronic health records research.NPJ Digit Med. 2022 Apr 8;5(1):47. doi: 10.1038/s41746-022-00590-0. NPJ Digit Med. 2022. PMID: 35396454 Free PMC article.
-
Externally validated digital decision support tool for time-to-osteoradionecrosis risk-stratification using right-censored multi-institutional observational cohorts.Radiother Oncol. 2025 Jun;207:110890. doi: 10.1016/j.radonc.2025.110890. Epub 2025 Apr 11. Radiother Oncol. 2025. PMID: 40222595 Free PMC article.
-
Characterization and validation of a prognostic model for the N6-methyladenosine-associated ferroptosis gene in colon adenocarcinoma.Transl Cancer Res. 2024 Aug 31;13(8):4389-4407. doi: 10.21037/tcr-24-88. Epub 2024 Aug 6. Transl Cancer Res. 2024. PMID: 39262465 Free PMC article.
References
-
- Harrell FE Jr. Regression Modeling Strategies. 2nd ed. New York, NY: Springer‐Verlag; 2015.
-
- Steyerberg EW. Clinical Prediction Models. 2nd ed. New York, NY: Springer‐Verlag; 2019.
-
- Cox DR. Two further applications of a model for binary regression. Biometrika. 1958;45(3–4):592‐565.
-
- Wilson PW, D'Agostino RB, Levy D, Belanger AM, Silbershatz H, Kannel WB. Prediction of coronary heart disease using risk factor categories. Circulation. 1998;97(18):1837‐1847. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
