Theoretical Bases for the Role of Red Blood Cell Shape in the Regulation of Its Volume
- PMID: 32581839
- PMCID: PMC7297144
- DOI: 10.3389/fphys.2020.00544
Theoretical Bases for the Role of Red Blood Cell Shape in the Regulation of Its Volume
Abstract
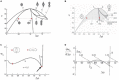
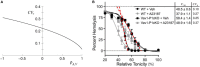
The red blood cell (RBC) membrane contains a mechanosensitive cation channel Piezo1 that is involved in RBC volume homeostasis. In a recent model of the mechanism of its action it was proposed that Piezo1 cation permeability responds to changes of the RBC shape. The aim here is to review in a descriptive manner different previous studies of RBC behavior that formed the basis for this proposal. These studies include the interpretation of RBC and vesicle shapes based on the minimization of membrane bending energy, the analyses of various consequences of compositional and structural features of RBC membrane, in particular of its membrane skeleton and its integral membrane proteins, and the modeling of the establishment of RBC volume. The proposed model of Piezo1 action is critically evaluated, and a perspective presented for solving some remaining experimental and theoretical problems. Part of the discussion is devoted to the usefulness of theoretical modeling in studies of the behavior of cell systems in general.
Keywords: Gárdos channel; Piezo1; cell to cell variability; curvature dependent protein–membrane interaction; mechanosensitivity; negative feedback loop; osmotic fragility; spectrin skeleton.
Copyright © 2020 Svetina.
Figures



References
-
- Ataullakhanov F. I., Korunova N. O., Spiridonov I. S., Pivovarov I. O., Kalyagina N. V., Martinov M. V. (2009). How erythrocyte volume is regulated, or what mathematical models can and cannot do for biology. Biochem. Mosc. Suppl. Ser. A Membr. Cell Biol. 3 101–115. 10.1134/s1990747809020019 - DOI
-
- Božič B., Kralj-Iglič V., Svetina S. (2006). Coupling between vesicle shape and lateral distribution of mobile membrane inclusions. Phys. Rev. E 73:041915. - PubMed
-
- Brumen M., Glaser R., Svetina S. (1979). Osmotic states of red blood cells. Bioelectrochem. Bioenerget. 6 227–241. 10.1016/0302-4598(79)87010-5 - DOI
-
- Brumen M., Glaser R., Svetina S. (1981). Study of the red blood cell osmotic behaviour in the “pump-leak” model. Period. Biol. 83 151–153.
Publication types
LinkOut - more resources
Full Text Sources

